時系列予測の手法別解説
【加重移動平均法(1/2)】
解析手法の役割
加重移動平均は時系列データの傾向を調べる解析手法で、季節不規則変動調整済み系列TCを算出します。TCIをTCで割ることによってIを算出します。
適用できるデータ形態と時期数
月次データ、四半期データ、年次データ、日別データなど全ての時間変数に適用できます。
データの時期数はどのデータ形態も4以上です。
具体例
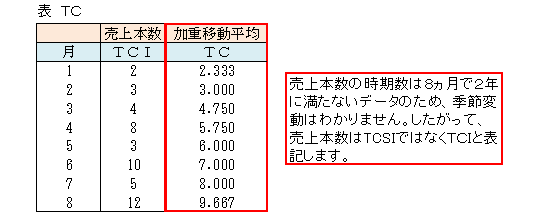
下記表は売上本数のデータです。

加重移動平均の求め方
移動平均同様、当該月の前後1ヵ月のデータを用いますが、平均を求める際、当該月を2倍した合計値を4で割って算出します。(2倍したデータを用いたので3ではなく4で割ります。)
2月の場合 (1月 + 2×2月 + 3月) ÷ 4ヵ月 =(2+2×3+4)÷4=3
3月の場合 (2月 + 2×3月 + 4月) ÷ 4ヵ月 =(3+2×4+8)÷4=4.75
3月の場合 (2月 + 2×3月 + 4月) ÷ 4ヵ月 =(3+2×4+8)÷4=4.75
前の月がない1月と後の月がない8月は、移動平均は計算できませんでしたが、加重移動平均は次のようにして求めることができます。
1月は前の月のデータがないので加重移動平均は次となります。
1月の場合 ( 2×1月 + 2月) ÷ 3ヵ月 =( 2×2+3 )÷3=2.333
8月は後の月のデータがないので加重移動平均は次となります。
8月の場合 (7月 + 2×8月 ) ÷ 3ヵ月 =( 5+2×12 )÷3=9.667
加重移動平均からわかること
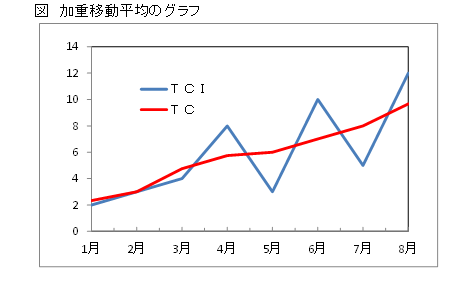
売上本数(TCI)と移動平均のグラフを重ね書きします。
TCの線はTCIの折れ線の真ん中を通り、TCの変動はTCIに比べ小さくなっています。したがって、TCはTCIに比べ売上本数の傾向が捉えやすくなっています。
移動平均に比べ、TCの線が滑らかになることが知られています。
移動平均は計算できない月がありましたが、加重移動平均は全ての月について計算できます。TCの把握は移動平均より加重移動平均で行うのがよいでしょう。
●留意点
移動の期間(3ヵ月間、3四半期間、3年間、・・・)を項数あるいはサイクルといいます。項数は3だけでなく、それ以上の加重移動平均を求めることができます。
項数が奇数、偶数どちらでも加重移動平均を算出できます。
項数が奇数と偶数で求め方が異なります。まず始めに、奇数の場合について説明します。
項数が奇数の場合
加重移動平均は、次に示すウエイトをデータに掛けて加重移動合計を算出し、加重移動合計をウエイト合計で割ることによって求められます。
ウエイトは加重移動平均を求める時期を最大とし、その時期から離れるに従い小さくなる値とします。
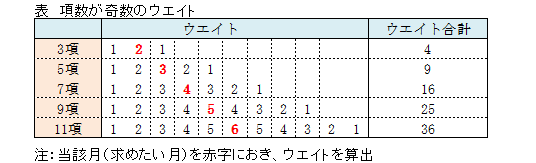
先ほどは3項の加重移動平均でした。ここでは下記データについて、5項の加重移動平均の算出方法を説明します。

<4月における5項加重移動平均>
4月 加重移動合計=1×2月 + 2×3月 + 3×4月 + 2×5月 + 1×6月
=1×3 + 2×4 + 3×8 + 2×3 + 1×10 =51
ウエイト合計=1+2+3+2+1=9
加重移動平均 = 加重移動合計 ÷ ウエイト合計=51÷9=5.667
時系列データの先頭あるいは末尾部分は、計算対象のデータが存在しないので、下記に示すような短縮加重を行うことによって、加重移動平均を算出します。
この例では、1月、2月、7月、8月が計算対象のデータが存在しません。
<2月における5項加重移動平均>
2月の短縮加重移動を示します。
2月 加重移動合計=2×1月 + 3×2月 + 2×3月 + 1×4月 ← 12月のデータ無し
=2×2 + 3×3 + 2×4 + 1×8 =29
ウエイト合計=2+3+2+1=8
加重移動平均= 加重移動合計 ÷ ウエイト合計=29÷8=3.625
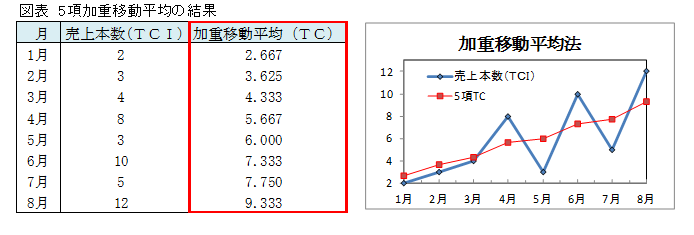
全ての月の加重移動平均を示します。
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。











