時系列予測の手法別解説
【月別平均法】
解析手法の役割
月別平均法は、時系列データの季節性を調べる解析手法で、季節変動指数Sと季節変動調整済み系列TCIを算出します。
適用できるデータ形態と時期数
月次データと四半期データに適用できます。
月次データの月数は24ヵ月以上、四半期データの期数は8期以上です。
具体例
下記表は住宅販売会社A営業支店における住宅の販売戸数のデータです。

季節変動指数Sの求め方
このデータで季節変動の求め方を説明します。
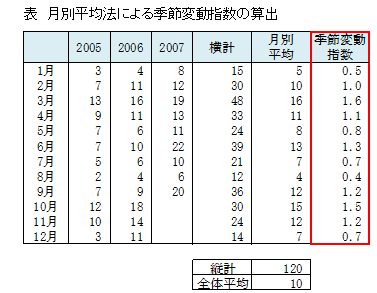
上記の販売戸数のデータ表を下記に示すように、月別年別のデータ表にします。
月ごとに横計と月別平均を算出します。
各月の月別平均を合計した値を12(ヵ月)で割り全体平均を求めると10(戸)です。月別平均を全体平均で割った値が季節変動指数Sです。
●留意点
・2年未満(月次は24ヵ月未満、四半期データは8期未満)のデータに月別平均法を適用した場合、そこから得られた季節変動指数Sは2年足らずのデータから求められたもので信憑性は薄く、適用しないのが通常です。
・季節変動指数はEPA法という解析手法でも算出できます。
・EPA法のSは毎年変化しますが、月別平均法のSは毎年同じです。
Sからわかること
・季節変動指数Sは1を基準に大きいと売れる月、小さいと売れない月と判断できます。
季節変動調整済み系列TCIの求め方
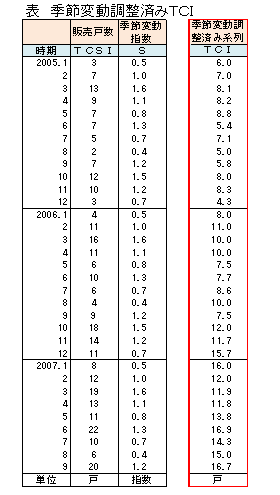
求められた12個の季節変動指数Sを右の表の該当する月の所に記入します。
販売戸数(TCSI)を季節変動指数(I)で割ることによって、季節変動調整済み系列TCIが求められます。
【計算例】 2005年1月のTCI=TCSI÷S=3÷0.5=6.0(戸)
他の月のTCIは右で示します。
TCIからわかること
季節変動調整済み系列TCIのグラフを描きます。
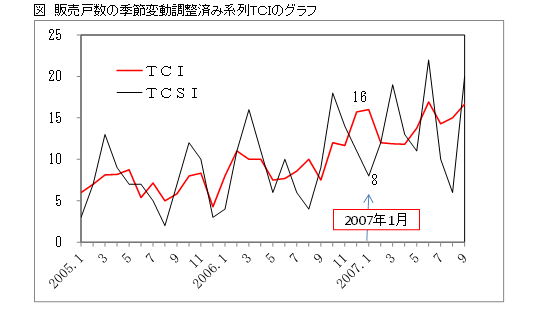
TCIは季節の影響を除去したところで、販売戸数が売れているかいないかが把握できます。
例えば、2007年1月の販売戸数は8戸と低い売上になっていますが、これは、1月は売れないという季節性によるものです。季節の影響を除去したTCIでは16戸となり、売れない1月にしては売れた(頑張った)ということです。
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。











