判別分析
《判別分析(1/2) 》
1.判別分析の基本
判別分析が適用できるテーマとデータ
判別分析は、目的変数がカテゴリーデータ(群データ)、説明変数が数量データの時、適用できる解析手法です。
判別分析が適用できるテーマと例題を示します。
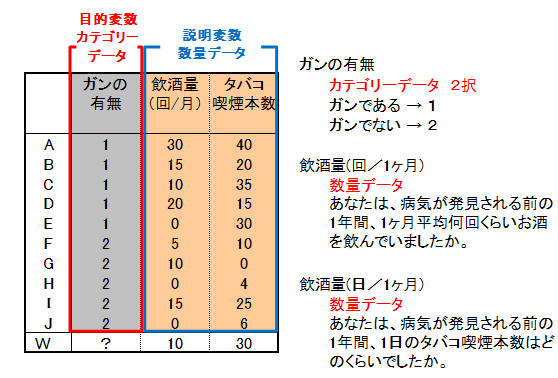
ガンの原因はいろいろな要素が考えられますが、ここでは例題なのでシンプルに、飲酒量、タバコ喫煙本数としましょう。
既に、ガンである、ガンでないと判定された人を対象に、飲酒量、タバコ喫煙本数を調べます。集められたデータから、ガン判別の関係式を作成し、現在ガンであるかないかが分からない人について、ガンの有無を判別(予測)することにします。
このとき収集したデータの形態を調べると、飲酒量、タバコ喫煙本数は説明変数で数量データ、ガンの有無は目的変数でカテゴリーデータです。これよりこのテーマには判別分析が適用されることになります。
判別分析から明らかにできること
判別分析は、目的変数と説明変数との関係を調べ関係式を作成し、その関係式を用いて次のことを明らかにする手法です。
①説明変数の重要度ランキング
②判別(予測)
データの制約条件
①ある説明変数のデータが全て同じ場合、判別分析は実行できません。
②任意の複数項目を選択し、個体ごとにその項目のデータの合計を計算したとき、どの個体も合計値が同じになる場合、判別分析は実行できません。
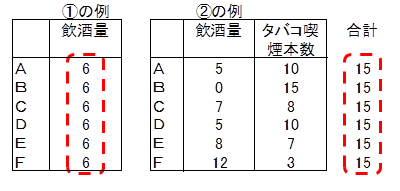
③判別分析に適用するデータは次式の条件を満たしてなければなりません。
個体数>説明変数の個数+1
ガンの有無について調べると、「説明変数の個数+1」は3です。従って個体数は4以上必要です。この例題の個体数は10人なので、このデータは判別分析が適用できます。
判別分析を行う前の基本分析
判別分析を行う前に基本解析を行います。
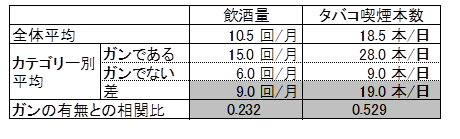
目的変数はカテゴリーなので、各カテゴリーの比率を算出します。
説明変数は数量データなので、基本統計量、度数分布を作成します。
目的変数と説明変数の関係を調べます。目的変数がカテゴリーデータ、説明変数が数量データなので、カテゴリー別平均値と相関比を算出します。カテゴリー別平均に差があるか、相関比の値が大きい説明変数は何かを検討してから多変量解析へ進みましょう。
判別分析で明らかにできること
判別分析は、目的変数と説明変数との関係を調べ関係式を作成し、その関係式を用いて次のことを明らかにする手法です。
①説明変数の重要度ランキング
②判別(予測)
残念ながらExcelには判別分析を処理する機能はありません。判別分析ができるソフトを用い、がん有無のデータに対して判別分析を実行し関係式を作成しました。

関係式の係数の求め方
関係式の係数はどのようにして求めるかを考えて見ましょう。
まず始めに、先生から皆さんへ問題をだします。
右記の□の中に適当な数値を代入し、全ての人において合計が、ガンで有る人はプラス、ガンでない人はマイナスになるようにしてください。
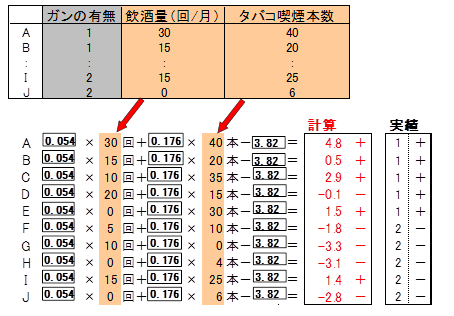
一つの解答例を上記に示しました。
この解答は、ガンであるA~Eさんの5人の内4人がプラス、ガンでないF~Jさんの5人の内4人がマイナスとなり、正解に近いと思われます。
重回帰分析や数量化Ⅰ類では、実績値と関係式から求められた理論値(サンプルスコア)ができるだけ一致するよう、すなわち実績値と理論値の相関ができるだけ大きくなるように、関係式の係数を求めました。
判別分析も同様な考え方で係数が求められます。
判別分析の実績値はガンの有無でカテゴリーデータです。上記で計算された値(理論値)を、判別分析では判別得点といいます。
実績値はカテゴリーデータ、判別得点は数量データなので両者の相関は相関比で求められます。
したがって、判別分析における関係式の係数は実績値(ガンの有無)と判別得点との相関比が最大となるように求めたものです。
関係式の係数を判別係数といいます。前述の関係式の判別係数は相関比を最大にする値です。
分析精度
分析精度を調べる方法を二つ示します。
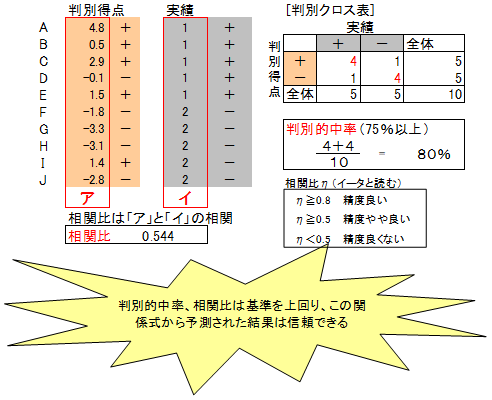
一つは、実績値(ガンの有無)と判別得点との相関比です。相関比の値が大きいほど分析精度は高く、基準の0.5を上回れば関係式は予測に使えると判断します。
相関比はいくつ以上あれば良いかと、よく質問されます。残念ながらいくつ以上あれば良いという統計学的基準はありません。この基準は、分析者が経験的な判断から決めることになります。先生は、下表のように決めていますが、皆さんはいかがでしょうか。
もう一つは、判別クロス表を用いる方法です。判別クロス表は、判別得点の符号「+、-」とガンの有無とをクロス集計したものです。下記の判別クロス集計表の赤表示の数値は実績と予測が一致した人数を示しています。一致人数の全人数に占める割合を判別的中率といいます。判別的中率の値が大きいほど分析精度は高く、基準の75%を上回れば関係式は予測に使えると判断します。
判別係数の検討
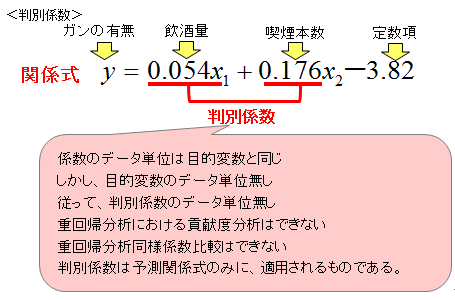
重回帰分析で、関係式の係数にはデータ単位があり目的変数のデータ単位と同じだということを学びました。
判別分析も同様に、目的変数と説明変数のデータ単位は同じです。ところが、判別分析の目的変数はカテゴリーデータでデータ単位がありません。したがって、説明変数もデータ単位がないということになります。
重回帰分析は目的変数、説明変数にデータ単位があったので、説明変数の目的変数に対する貢献度の分析ができましたが、判別分析は各変数にデータ単位がないので貢献度の分析はできません。
各変数の重要度
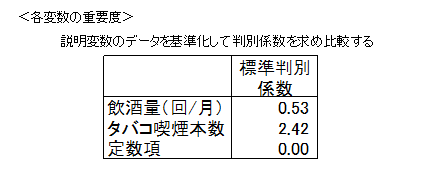
ガンの有無のデータを基準値にして判別分析を行います。求められた係数を標準判別係数といいます。
ガンの有無データの関係式の飲酒量0.054とタバコ喫煙本数0.176とを比較し、飲酒量の係数の方が小さいから重要でないということはいえません。標準回帰係数では、飲酒料0.53とタバコ喫煙本数2.42とを比較し、タバコ喫煙本数の係数の方が大きいので重要であるという判断をします。
注.基準値データで判別分析を行うと定数項は必ず0になります。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。











