コンジョイント分析
《コンジョイント分析(1/3) 》
1.コンジョイントカードの作成方法、評価方法
コンジョイント分析とはどのような手法か
通常、消費者は商品の購入(あるいは選択)をするとき、その商品の機能やサービスなどの複数の項目を1つずつ検討し、検討した評価項目を組み合わせて総合的に、購入の有無を判断します。
例えば、ある人がマンションを購入する場合、駅からの時間、駐車場の有無、価格を考えたとします。△△物件は「駅から5分未満」、「駐車場あり」なので、魅力的なマンションといえますが、価格が高く、そのマンションの総合的評価は購入度合としては低い評価がされたとしましょう。この人は、数多くある評価項目の中で価格(が高すぎる)を最も重視して、総合評価を決めたことになります。
コンジョイント分析は、上記に示したような商品の総合評価をする時、すなわち消費者が複数の商品から1つを選ぶ場合、それぞれの評価項目がどの程度目的変数(購入度合)に影響を与えているかを明らかにする分析手法です。
目的変数への影響度は、相関分析や重回帰分析でも明らかにできます。これらの手法とコンジョイント分析とでは把握内容は同じですが、データ収集(調査)する部分で大きな違いがあります。
コンジョイント分析は、調査回答者に対して、商品の特性を組み合わせたコンジョイントカード(商品完成予想図)を複数提示し、コンジョイントカードに対する評価をとります。
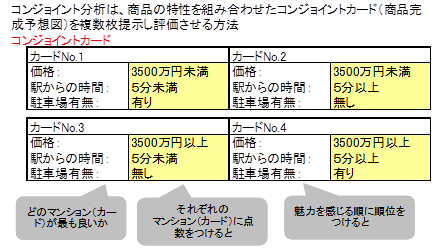
コンジョイントカード/商品完成予想図
マンションの例では、カードNo.1は「価格:3500万円未満、駅からの時間:5分未満、駐車場有無:無し」、カードNo.2は「価格:3500万円未満、駅からの時間:5分以上、駐車場有無:有り」、・・・などです。
評価は、コンジョイントカードに得点をつける、好きな順での並べ替える、などによって行います。
従来の調査方法は、「駅からの時間は5分未満、5分以上、どちらを重視しますか」など、各項目ごとに質問をしましたが、コンジョイント分析は、項目を結合したコンジョイントカードを評価させるところが特徴です。
なお、コンジョイントを英和辞典で調べると「結合」と表記されています。コンジョイント分析は項目を結合してカードを作成することから、このような名称となりました。
コンジョイント分析はどのような手法であるかを、一言でいうならば、コンジョイントカードに対する評価から、消費者が商品を購入(選択)する場合に最も重視している評価項目を把握したり、どの組み合わせ(コンジョイントカード)が最も良いかを明らかにしたりする手法です。
コンジョイントカードの枚数
コンジョイント分析で、最初にすることはコンジョイントカードを作成することです。
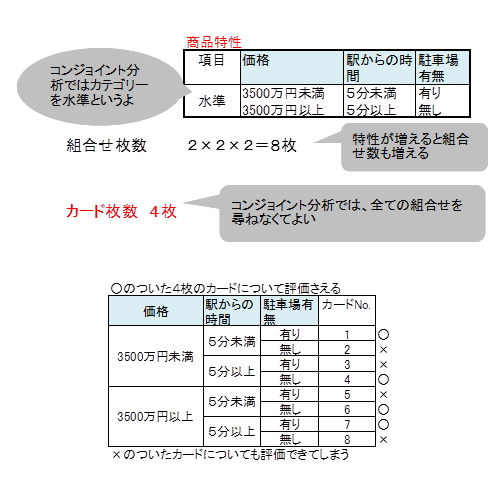
評価してもらう商品特性の項目とカテゴリーを設定します。なお、コンジョイント分析では、カテゴリーのことを水準といいますので、コンジョイント分析の学習においては水準という用語を用いることにします。
下記に、マンションの商品特性の項目と水準を示します。
マンションの例におけるコンジョイントカードは3特性の組み合わせによって作られますので、組み合わせの数は2×2×2=8で、カードの枚数は8枚になります。
8枚のカードを評価で順序づけるとういことは可能ですが、特性が一つ増えると(例えば建物の方角)、用意すべきカードの枚数は一挙に16枚になってしまいます。16枚のカードを順序づけするのはとても難しいと思います。
コンジョイント分析の素晴らしいところは、16枚のカード全てについて評価してもらう必要がないということです。一部分だけのカードを作成しそれについての評価を求めれば、評価されていないカードについても、あたかも評価されたと同様の解析ができます。
この例の組合せ枚数は8枚ですが、コンジョイント分析を適用すると4枚のカードの評価で、8枚評価した解析と同じ結論をえることができます。
直交表
マンションの例は本来8枚のカードで調査しなければいけないところ、4枚のコンジョイントカードで調査すればよいことを示したものです。
4枚のカードは分析者の好みのカードで選ばれるものでなく、あるルールに従って選ばなければなりません。これからそのルールについて学ぶのですが、そのためには「直交表」について理解しなければなりません。
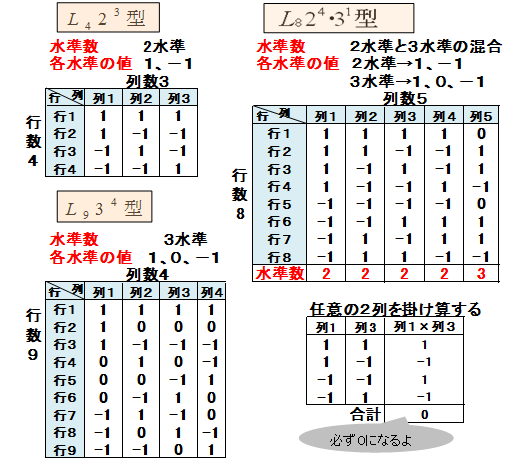
直交表にはいくつかの種類がありますが、下記はよく使用される直交表です。直交表にはそれぞれL4 23 型といった名前がつけられています。名前の中の数値は表の行数、列数、水準数を示しています。
直交表は、表内の任意の2列の数値を掛け合わせて、その答えを合計すると必ず0になります。また、任意の2列の単相関係数を計算すると必ず0になります。
直交表はいろいろな場面で利用されますが、コンジョイント分析に適用した場合、直交表の行数はコンジョイントカードの枚数となります。一つのテーマで複数の直交表が当てはまる場合がありますが、その場合は行数(カード枚数)の少ない直交表を適用します。