《共分散構造分析(7/7) 》
多母集団の同時分析モデル
≪例題7≫
下記のデータは、ある会社の6つの営業所におけるA製品とB製品の売上額、広告費、販売員数です。
製品の違いによって、売上に対する営業活動の影響度が違うように思われます。
両製品の営業活動の違いを明確にしてください。
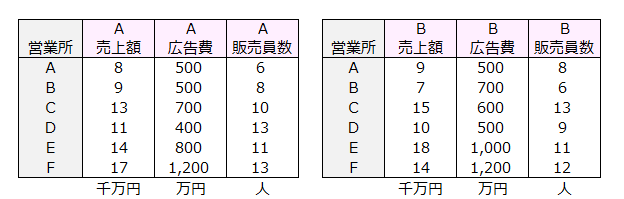
多母集団の同時分析モデルは、2つの母集団の因果関係の構図、違いを明確にする方法です。
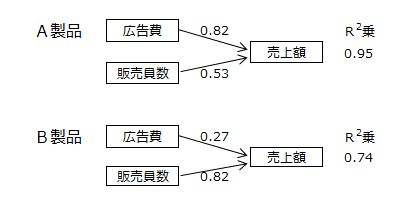
A製品は広告費の効果、B製品は販売員数の効果が顕著で、両者の営業活動のあり方に違いが見られました。
パス係数算出方法
どのような考え方でパス係数を求めているかを例題1で説明します。
パス図において、Pから始まりYに到達する経路はA,B,Cの3つあります。
この経路のパス係数の合計値がPとYの単相関係数とほぼ一致するようにパス係数が定められます。
パス係数Aはパス係数P→RとR→Yの積、パス係数Cはパス係数P→QとQ→Yの積で表します。パス係数BはP→Yが一つなのでのパス係数そのものとします。
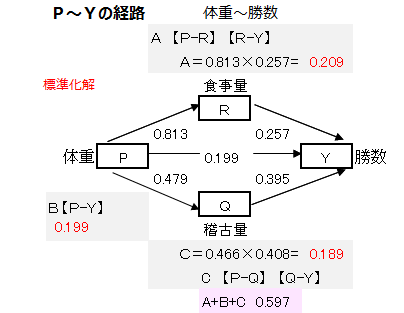
上記の計算を表にまとめました。
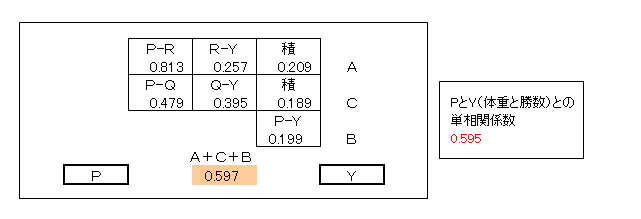
この経路の「パス係数の合計値」と「PとYの単相関係数」とはほぼ一致しています。
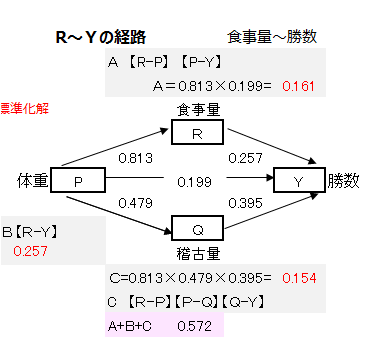
パス図において、Rから始まりYに到達する経路はA,B,Cの3つあります。
この経路のパス係数の合計値がRとYの単相関係数とほぼ一致するようにパス係数が定められます。
パス係数Aはパス係数R→PとP→Yの積、パス係数Cはパス係数R→PとP→QとQ→Yの積で表します。パス係数BはR→Yが一つなのでのパス係数そのものとします。
上記の計算を表にまとめました。
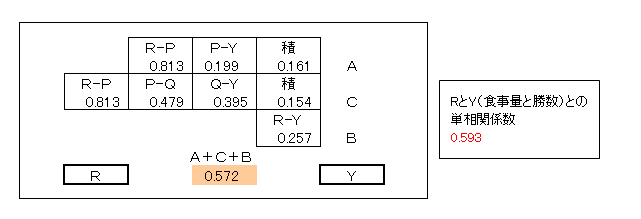
この経路の「パス係数の合計値」と「RとYの単相関係数」とはほぼ一致しています。
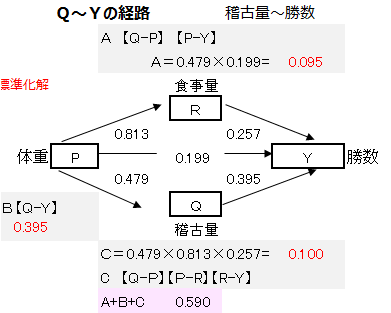
上記の計算を表にまとめました。
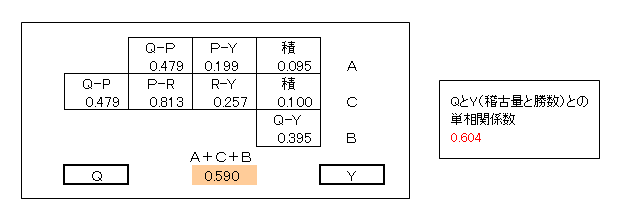
この経路の「パス係数の合計値」と「QとYの単相関係数」とはほぼ一致しています。
パス係数は、どの経路について求められたパス係数の合計値(理論的な相関係数)」と実際の相関係数ができるだけ近くなるように求められた値です。
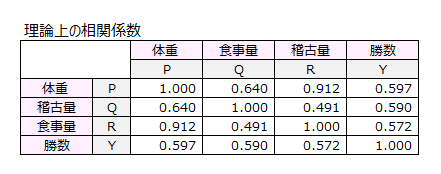
P~Y、Q~Y、R~Yについての経路を調べてきましたが、P~Q、Q~R、P~Rについても理論上の相関係数を求めました。下記はその結果を表にまとめたものです。
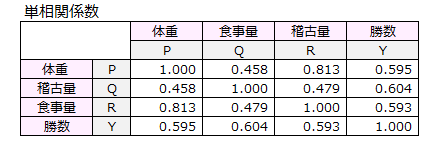
観測変数相互の単相関係数を算出しました。
上表と下表の相関係数の差分を求めました。
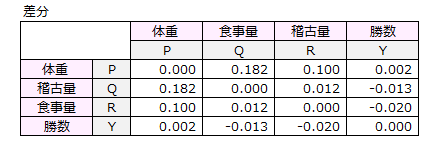
各セルの値ができるだけ0になるようにパス係数は算出されます。
観測データの分散共分散行列を求めます。
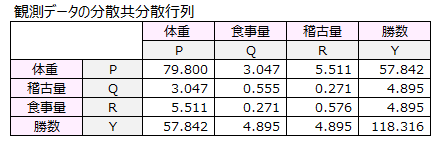
共分散分析が計算する理論上の分散共分散行列を求めます。
これら値は、上記で求めた理論上の相関係数に標準偏差を掛けることによって求められます。
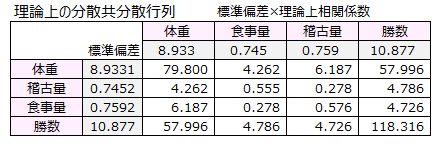
共分散構造分析は、2つの分散共分散行列ができるだけ近くなるようにパス係数を求める解析手法です。このことから解析手法名は共分散構造分析とネーミングされています。
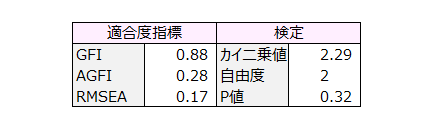
なお適合度指標は、2つの分散共分散行列の一致度を計算したものです。
観測変数における分散共分散行列をS、理論上の分散共分散行列をΣとします。
5つの変数名をx1、x2、x3、x4、x5とします。
Sを次の行列とします。
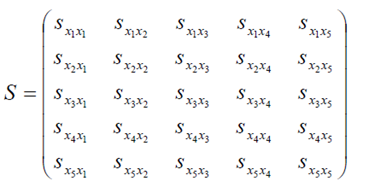
Σを次とします。
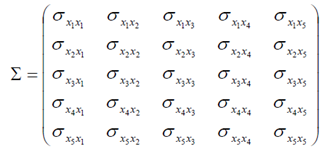
次の式を定義します。

-1逆行列、traceは対角行列の和です。
Lの値が最小になるように、最尤法によってパス係数を算出します。
パス係数の検定
各パスについての有意性をZ検定によって行います。
z値が1.96以上であれば有意と判断します。
LM検定(Lagrange Multiplier Test)とワルド検定(WALD TEST)はパス係数の検定方法で、矢印を増やしたり減らしたりしてよりよいパス図を描くための手法です。
・LM検定
LM 検定は、パスを増やすならどこにするかを検討するための検定です。重回帰分析 における変数増加法のようなものです。 具体的には、ある変数間に新たに矢印を引くか否かを適合度指標(GFI、カイ2乗値)の変化から検討します。
・ワルド検定
ワルド検定は、すでに引いてあるパスを減らすならどこにすべきかを検討するための検定方法です。重回帰分析における変数減少法のようなものです。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










