《共分散構造分析(2/7) 》
共分散構造分析とは
共分散構造分析(SEM)は、アンケート調査の回答データ、テスト得点、実験データなどの観測データにおいて、分析者が項目間(変数間)の因果関係について仮説を立て、これが正しいかどうかを検証する解析手法です。
共分散構造分析から次のことが把握できます。
・ 項目間の相関関係、因果関係を解明します。
・ 潜在変数を導入することによって、潜在変数と項目との間の因果関係を解明します。
・ 潜在変数から、類似した傾向を示す項目をまとめることができます。
・ 潜在変数の間で因果関係を検討すれば、多くの項目の間の関係を直接扱うより効率よく扱えます。
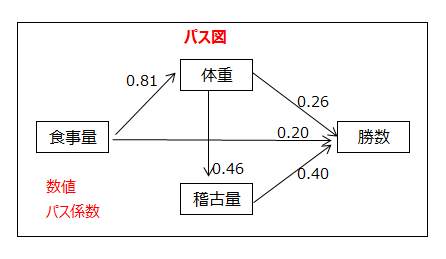
因果関係の仮説は項目間を矢印で結んだパス図と呼ばれる図で表します。共分散構造分析を行うことにより、項目間の関係の強さを表すパス係数と呼ばれる値が求められ、パス図の矢印線上に記載されます。パス係数の大小によって因果関係を解明します。
「共分散構造分析」という名称は、Covariance Structure Analysisを訳したものです。「共分散構造分析」という名称は「共分散」や「分散」を連想させますが、この手法での本論でないので「構造方程式モデリング」と呼ばれる傾向にあります。「構造方程式モデリング」という名称は、Structural Equation Modelingを訳したものです。頭文字をとって「SEM」と呼ばれることもあります。
パス図
パス図に適用する図形について説明します。
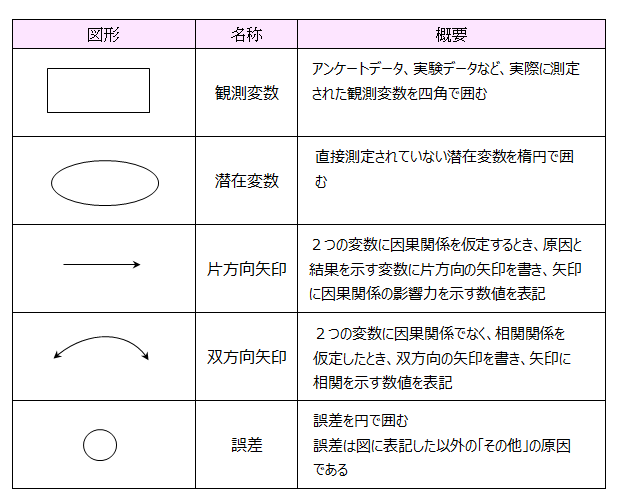
【例】
パス係数
パス係数は変数間の相関関係、因果関係を表す値です。パス係数には標準化解と非標準化解の2種類があります。
標準化解はすべての観測変数と潜在変数の分散を1に基準化して求めたときの値、非標準化解は基準化しないそのままのデータについて求めたときの値です。分かりやすい例として重回帰分析を取り上げると、回帰係数は非標準化解、標準回帰係数は標準化解です。
パス係数の強さを解明するときは標準化解、大きさを解明するときは非標準化解を用います。
下記の上図のパス係数は例題1の標準化解、下図のパス係数は非標準化解です。
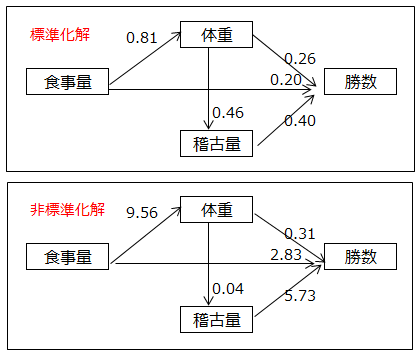
・標準化解の解釈
体重→勝数、食事量→勝数、稽古量→勝数のパス係数をみると、0.26、0.20、0.40です。
勝数への影響度が最も強いのは稽古量、次に体重、食事量が続きます。
・非標準化解の解釈
稽古量と食事量のデータは「多い」「普通」「少ない」の3段階です。稽古量が1段階増えると勝数は5.73勝増える、食事量が1段階増えると2.83勝増えることを意味しています。
体重から勝数への係数は0.31で、食事量が一定であるならば、体重が1kg増えると勝数は0.31勝増えることを示しています。
・直接効果と間接効果
食事量から勝数へのパスは2経路あります。
「食事量→勝数」の直接パスと、「食事量→体重→勝数」の体重を経由する間接パスです。
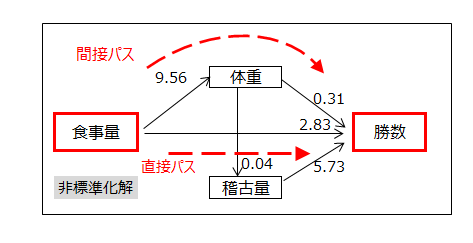
直接パスは、体重を経由しない、つまり、体重が一定であるとき、食事量が1段階増えたときの勝数は2.83勝増えることを意味しています。これを直接効果といいます。
間接パスについてみてみます。
食事量から体重への係数は9.56で、食事量が1段階増えると体重は9.56kg増えることを示しています。
体重から勝数への係数は0.31で、食事量が一定であるならば、体重が1kg増えると勝数は0.31勝増えることを示しています。
食事量が1段階増加したときの体重を経由する勝数への効果は
9.56×0.31=2.96
と推定できます。これを食事量から勝数への間接効果といいます。
この解析から、食事量から勝数への総合効果は
直接効果+間接効果=総合効果
で計算できます。
2.83+2.96=5.79
となります。
この式より、食事量の勝数への総合効果は、食事量を1段階増やすと、平均的に見て5.79勝、増えることが分かります。
・外生変数と内生変数
パス図のモデルの中で、どこからも影響を受けていない変数のことを外生変数といいます。他の変数から一度でも影響を受けている変数のことを内生変数といいます。
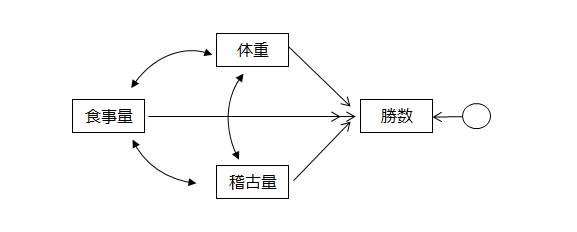
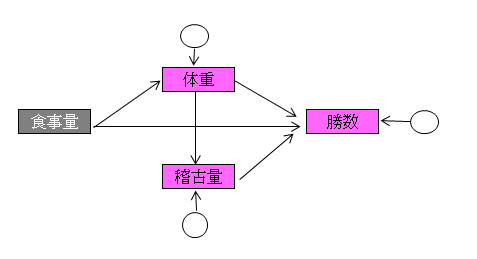
下記パス図において、食事量は外生変数(灰色)、体重、稽古量、勝数は内生変数(ピンク色)です。
内生変数は矢印で結ばれた変数以外の影響も受けており、その要因を誤差変動として円で示します。したがって、内生変数には必ず円(誤差変動)が付きますが、パス図を描くときは省略しても構いません。
適合度指標
パス図における矢印は仮説に基づいて引きますが、仮説が明確でなくても矢印は適当に引くことができます。したがって、引いた矢印の妥当性を調べなければなりません。そこで登場するのがモデルの適合度指標です。
パス係数と相関係数は密接な関係がり、適合度は両者の整合性や近さを把握するためのものです。具体的には、パス係数を掛けあわせ加算して求めた理論的な相関係数と実際の相関係数との近さ(適合度)を計ります。近さを指標で表した値が適合度指標です。
良く使われる適合度の指標は、GFI、AGFI、RMSEA、カイ2乗値です。
GFIは重回帰分析における決定係数(R2)、AGFIは自由度修正済み決定係数をイメージしてください。GFI、AGFIともに0~1の間の値で、0.9以上なら矢印の引き方が妥当、良いモデル(理論的相関係数と実際の相関係数が近いモデル)といえます。
GFI≧AGFIという関係があります。GFIに比べてAGFIが著しく低下する場合は、あまり好ましいモデルといえません。
RMSEAはGFIの逆で0.1未満なら良いモデルといえます。
これらの基準は絶対的なものでなく、GFIが0.9を下回ってもモデルを採択する場合があります。GFIは、色々な矢印でパス図を描き、この中でGFIが最大となるモデルを採択するときに有効です。
カイ2乗値は0以上の値です。値が小さいほど良いモデルです。カイ2乗値を用いて、母集団においてパス図が適用できるかを検定することができます。p値が0.05以上は母集団においてパス図は適用できると判断します。
例題1のパス図の適合度指標を示します。
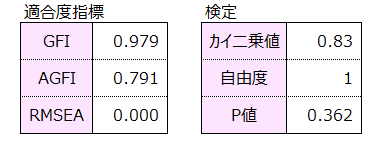
GFI>0.9、RMSEA<0.1より、矢印の引き方は妥当で因果関係を的確に表している良いモデルといえます。カイ2乗値は0.83でカイ2乗検定を行うとp値>0.05となり、このモデルは母集団において適用できるといえます。
※留意点
カイ2乗検定の帰無仮説と対立仮説は次となります。
・帰無仮説
項目間の相関係数とパス係数を掛け合わせて求められる理論的相関係数は同じ
・対立仮説
項目間の相関係数とパス係数を掛け合わせて求められる理論的相関係数は異なる
p値≧0.05だと、帰無仮説は棄却できず、対立仮説を採択できません。したがってp値が0.5以上だと実際の相関係数と理論的な相関係数は異なるといえない、すなわち同じと判断します。