《共分散構造分析(3/7) 》
自由度
自由度を次の式によって定義します。

上記パス図の自由度を求めます。
K=4 K(K+1)/2=4×5÷2=10 m=5+1+3+0=9
自由度=10-9=1
自由度が0のモデルを飽和モデルといいます。
飽和モデルは、矢印をどのように引いても、適合度指標は必ず1になります。
カイ2乗値は必ず0になります。
飽和モデルの場合、適合度指標の活用、検定はできませんがパス図は有効です。
自由度がマイナスになるとパス図が作成できないことがあります。
パス図の検討
例題1について、変数間の因果関係が定かでないとして、色々なパス図を描き、この中から最適なパス図を探してみます。
作成したパス図は11個です。パス図のパス係数は標準化解です。非標準化解、適合度指標、カイ2乗検定についても記載しました。
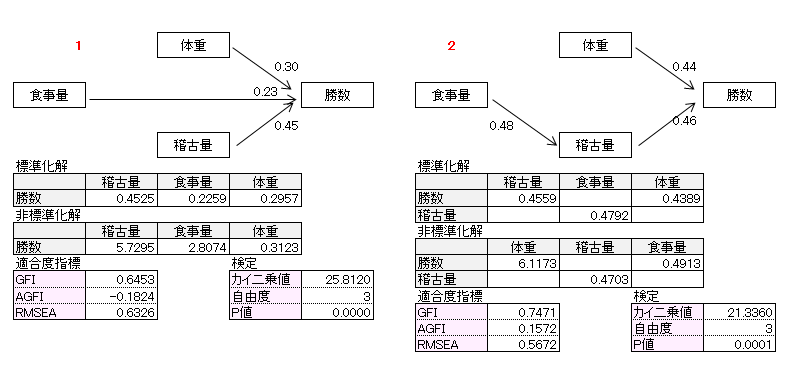
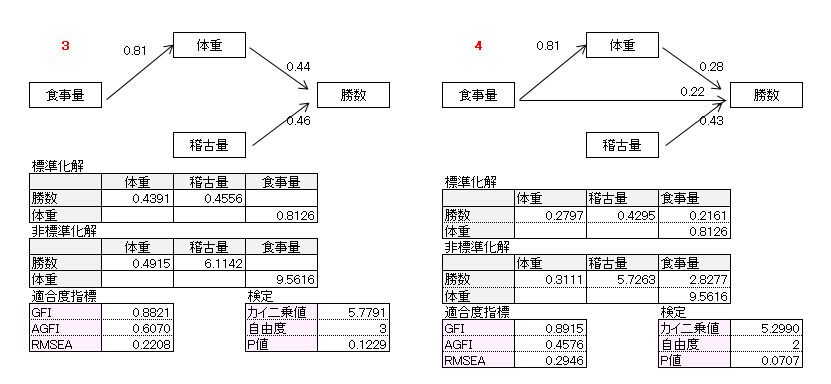
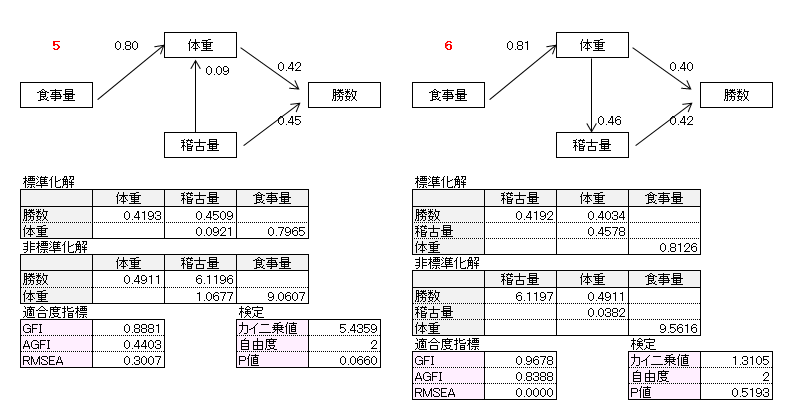
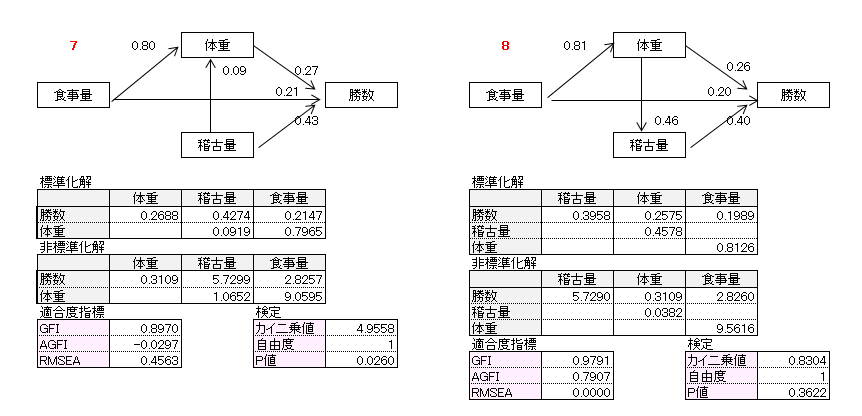
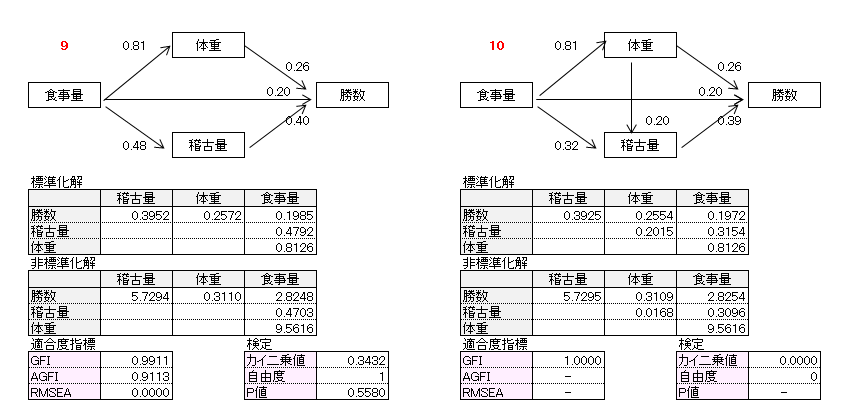
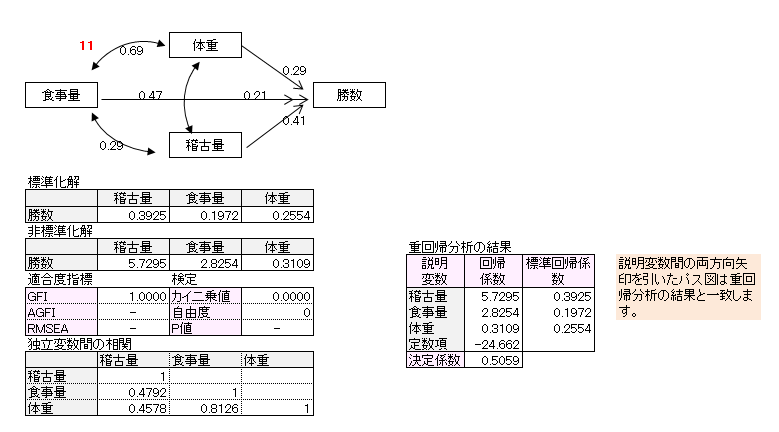
10番目パス図、11番目パス図の自由度は0(飽和モデル)で適合度指標、カイ2乗値が算出されないので、この例題では検討パス図から外しました。
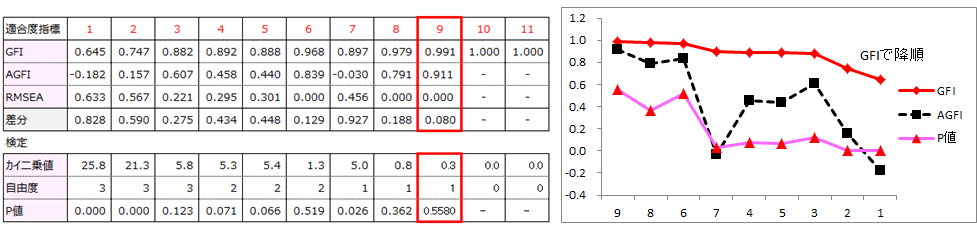
残り9個のGFI、AGFI、p値の一覧表、グラフを作成しました。
GFIが最大、GFIとAGFIの差分が最小、p値が最大のパス図が最適といえるので、9番目パス図を最適解とします。