《共分散構造分析(6/7) 》
事例2:重回帰分析型モデル
≪例題5≫
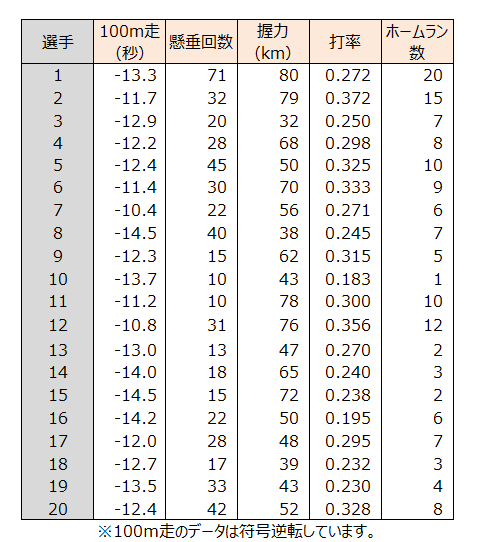
野球選手20人について、100m走、懸垂回数、握力の体力測定値と打率、ホームラン数の成績を調べました。打率やホームラン数の成績を上げるために重要な体力は何かを調べてみましょう。
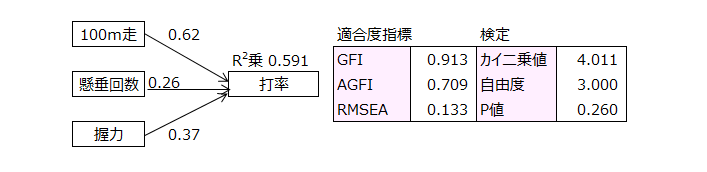
(1)目的変数は打率、説明変数は100m走、懸垂回数、握力で、説明変数間の相関がないと仮定する重回帰分析を行います。
回帰係数(パス係数)と決定係数R2 (R2乗)が出力されます。
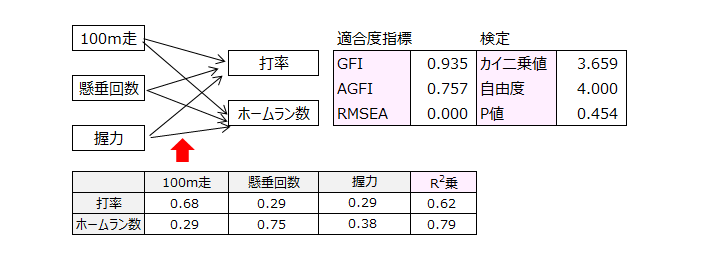
(2)目的変数は打率、説明変数は100m走、懸垂回数、握力で、説明変数間の相関があると仮定します。(双方向の矢印を引くと重回帰分析の結果と一致。) 自由度0(飽和モデル)で、適合度指標、検定は行えません
この結果は、解析手法「重回帰分析」の結果と一致します。

(3)目的変数は打率とホームラン数、説明変数は100m走、懸垂回数、握力で、説明変数間の相関がないと仮定します。
(4)目的変数は打率とホームラン数、説明変数は100m走、懸垂回数、握力で、説明変数間の相関があると仮定します。
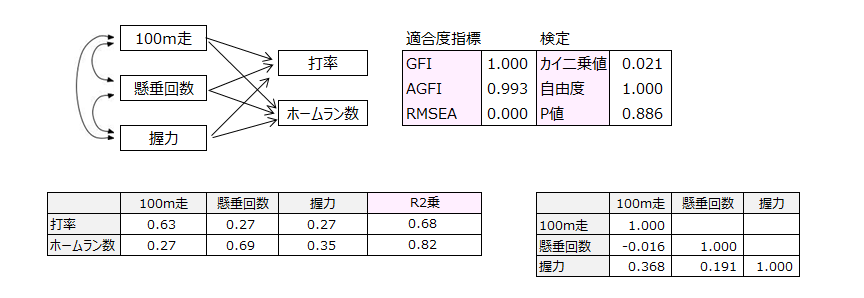
事例3 媒介プロセス重回帰分析モデル
[A]が[B]に,[A][B]が[C]に影響を及ぼす,といった形の重回帰分析をすることがあります。
例題1のデータについて、パス図を描くと次になります。

食事量が増えると体重が増え、食事量や体重が増えると稽古量が増え、食事量、体重、稽古量が増えると勝数が増えると解釈できます。
GFIは0.9をやや下回っていますが、決定係数は基準としている0.5を上回り、このパス図は、力士が勝数を増やすための教訓となります。
媒介プロセスの因果関係のたとえを紹介します。
| 【風が吹けば桶屋が儲かる】 風が吹けば砂埃のために目を病む人が多くなり、目を病んだせいで失明すれば音曲で生計を立てようとするから三味線を習う人が増え、三味線の胴に張る猫の皮の需要が増えます。 そのため、猫の数が減少し、猫が減れば猫が捕まえる鼠の数が増えます。鼠は桶をかじるから桶がよく売れるようになり、桶屋が儲かることから、桶屋が儲かる因果関係をいった昔話からでたことばです。 |
事例4:因子分析型モデル
≪例題6≫
新人タレントを採用するために、芸能プロダクションはいろいろなオーディションを行っています。
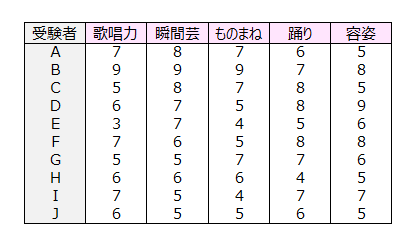
下記の表は、あるオーディションにおける受験者の歌唱力、瞬間芸、ものまね、踊り、容姿の成績(10点満点評価)を示したものです。
この成績から、各人のタレントとしての総合能力、アイドル系・お笑い系の能力を把握し、採用の有無、採用後のキャラクター作りの決定を判断したいと思います。
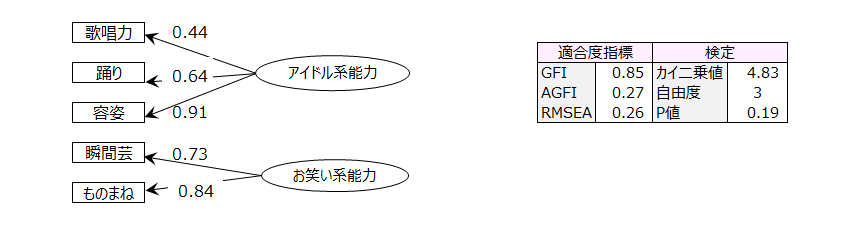
検証的因子分析を行います。
因子分析の回転には直交回転と斜交回転が有ります。前者は因子間(潜在変数間)の相関が0である、後者は0でないことを仮定しています、
まず始めに直交回転の検証的因子分析を行います。
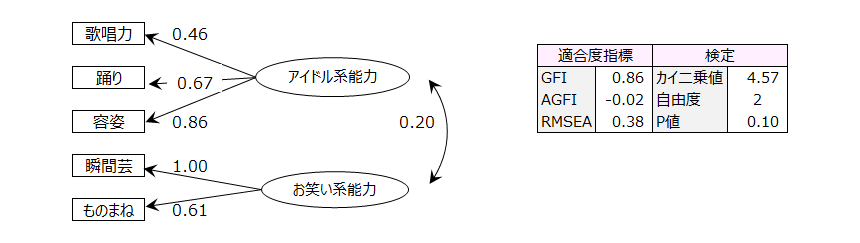
斜交回転の検証的因子分析を行います。
因子間を双方向の矢印で結ぶと斜交回転となります。
総合能力の因子を追加して、直交回転の検証的因子分析を行います。
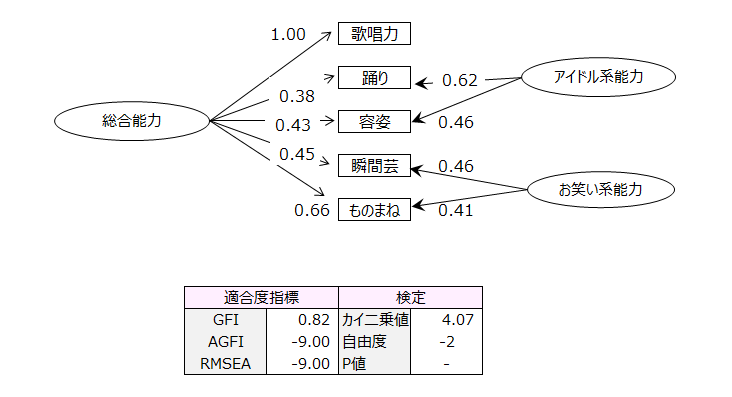
自由度はマイナスなので検定はできませんが、パス係数の解釈はできます。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










