共分散構造分析(SEM)
《共分散構造分析(1/7) 》
共分散構造分析(SEM)を知るための2つの例題
≪例題1≫
大相撲は1年間に6場所あります。
1場所15日間なので1年間の総日数は90日です。
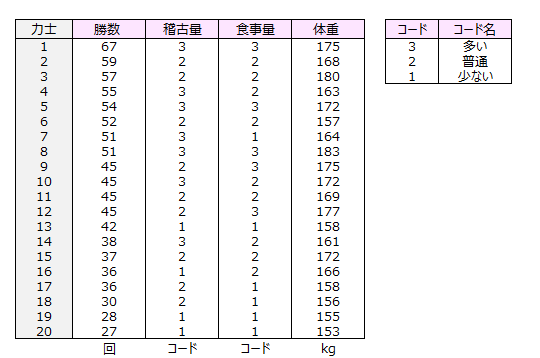
ある年について、90日間休場しなかった力士20人の勝数を調べました。
力士の稽古量、食事量、体重についても調べました。
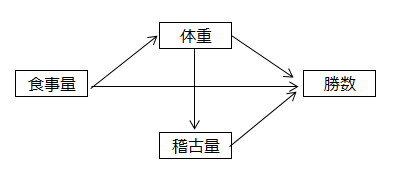
このデータに基づき、「食事量を増やすほど体重は重くなり、体重や稽古量が多い力士は勝数が増える」という仮説を検証したいと思います。
≪例題2≫
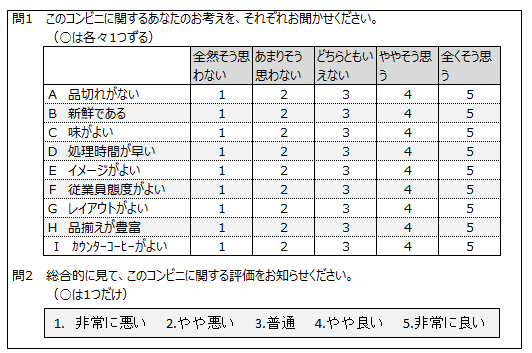
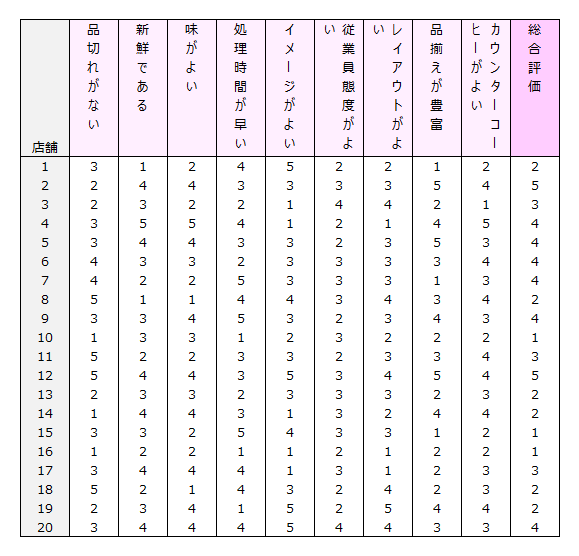
次の質問紙で、コンビニに来店した人にアンケート調査を行いました。

回答データ

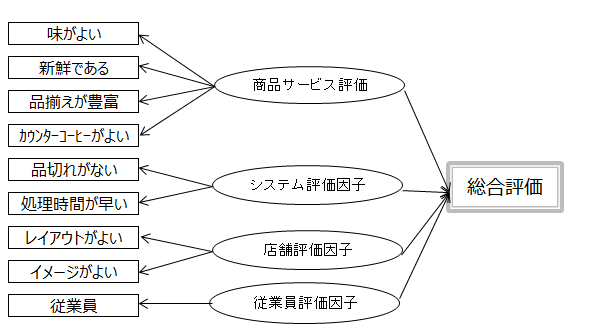
コンビニの総合満足度は、4つの因子(潜在変数)で説明できるとして、次の因果関係を示す図を作成しました。この仮説を検証しなさい。

・観測変数と潜在変数
アンケート調査の回答データや実験で測定されたデータを観測変数といいます。
コンビニ評価の4因子(商品サービス評価因子、システム評価因子、・・・)は回答(測定)されたデータでなく、統計解析の計算式によって創りだれるものです。計算式によって創り出されたデータを潜在変数といいます。
テスト成績を例にすると、国語や数学の得点は観測変数です。文系能力や理系能力のテスト科目は存在せず、これらの能力は、国語や数学の得点から計算されるものなので潜在変数です。
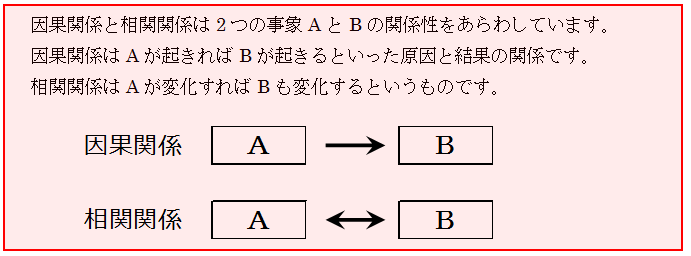
・因果関係と相関関係
因果関係は、項目間に原因と結果の関係があると言い切れる関係を意味しています。
例題1についてみると、大相撲の世界では「稽古量を増やすと勝数が多くなる」が通説です。「稽古量を増やす」という行為が原因で、「勝数が多くなる」という結果が導かれるので、両者の関係は因果関係です。
原因と結果の関係は、「原因→結果」という一方通行です。原因と結果に時間的順序が成り立っています。
食事量と稽古量の関係は、食事量を増やすと稽古量が増えるのか、稽古量を増やすと食事量が増えるか分からないので、両者の因果関係は定かでありません。両者に因果関係があるかは、これから学ぶ共分散構造分析で解明することができます。
因果関係があれば必ず相関関係は認められますが、相関関係があるからといって必ずしも因果関係は認められません。