
3.1 分散と標準偏差 ~飴作りでガチンコ勝負~

ばらばらの飴
バラツキを表す標準偏差
店長は莉子の説明に納得したものの、ちょっとすっきりしない点がありました。
店長:これから英太郎がどんどんうまくなったら、ヒストグラムでの比較はむずかしくなってしまうよね。
莉子:確かにそうですね。ヒストグラムの形状で判断するわけだから、比較は明らかに異なる場合でないと難しそう。他の方法はないか、先生に聞いてきます。
莉子:度数分布表やヒストグラムを作ることによってバラツキをみることができることはよく分かりました。でも比較をしたい場合、バラツキを表やグラフじゃなくて平均値みたいな数字で表せるといいと思うんですけど。
先生:バラツキは標準偏差という値で表すことができるよ。平均値が普段の生活でとっても役立っているように、統計の世界では標準偏差がとっても大切なんだ。 データが平均値付近に集まっているほど標準偏差は小さく、離れているほど大きくなる。
莉子:じゃあ、店長の作った飴の標準偏差の方が英太郎のよりも小さくなるってことですね。
先生:多分、そうなるだろうね。実際に計算してたしかめてみるといいよ。まずは簡単なデータで計算手順を説明しよう。
標準偏差の例
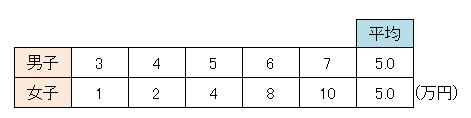
次のデータは男女5人の1カ月のアルバイト代です。平均は男女どちらも5万円ですが、男子は3~7万、女子は1~10万で、女子の方がバラツキが大きいと思われます。
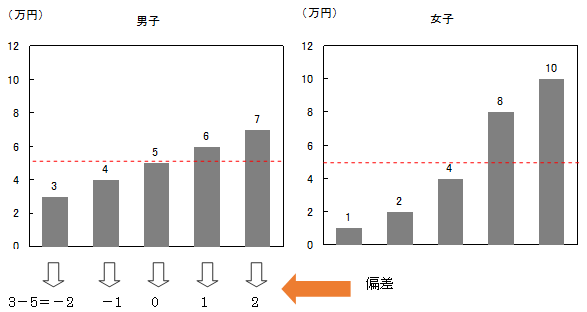
まずは一人ずつ、平均(5万円)との差をとってみましょう。この値を偏差といいます。
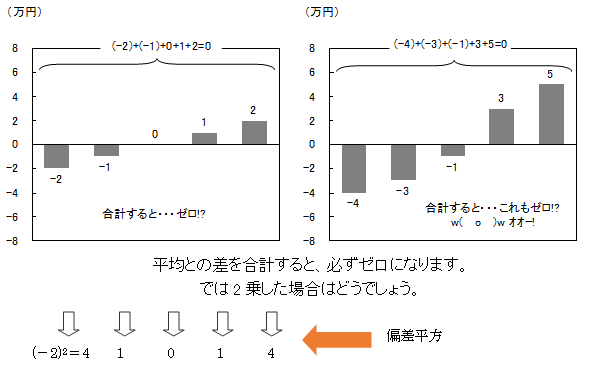
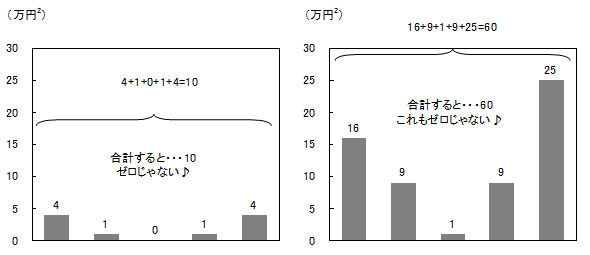
偏差平方の合計はゼロでなくなりました。偏差平方の合計を偏差平方和といいます。偏差平方和は人数が多いほど大きい値になるので、人数に影響を受けないように、一人当たりの値に変換します。

男子:2、 女子:12 (万円2)
これがバラツキを表す分散と呼ばれる値です。
先ほど2乗したので、今度はルート(平方根)※をとって元に戻します。
ルートをとることで、単位も「万円」に戻ります。
男子:1.41、女子:3.46 (万円)
これが標準偏差です。
分散もバラツキを表しますが、仕事で使うのは標準偏差の方が多いかもしれません。
標準偏差の値は男子よりも女子の値が大きいので、女子のバイト代の方がばらつきが大きいといえます。※「3の2乗」は9です。「9のルート」は3です。2乗とルートは相対する関係にあります。
すぐに使える!!統計入門
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。









