時系列予測の手法別解説
【タイムラグ相関】
解析手法の役割
時系列データの場合、1ヵ月前の営業活動が当月の売上に影響を及ぼしている場合があります。タイムラグ相関係数はタイムラグ(月をずらす)をとって、売上と規定要因の関係を調べる解析手法です。
適用できるデータ形態と時期数
月次データ、四半期データ、年次データ、日別データなど全ての時間変数に適用できます。データの時期数はどのデータ形態も4以上です。
具体例
下記表は売上と広告費のデータです。
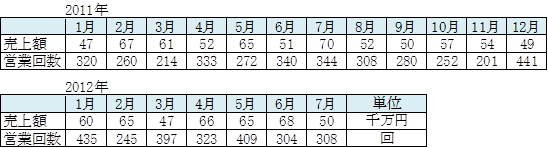
タイムラグ相関係数の求め方
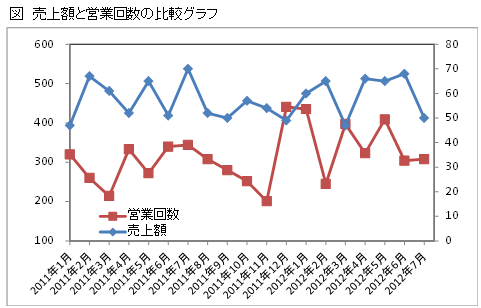
営業回数が売上規定要因であるかを調べるために時系列グラフを描きました。
ほとんどの月で営業回数が増加すれば売上額も増加(営業回数が減少すれば売上額が減少)という傾向が見られません。
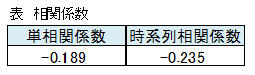
単相関係数、時系列相関係数は下記に示すようにマイナスの値となり、営業回数は売上予測をする上で重要な説明変数にならないと思われます。
前の月の営業回数と今月の売上額を比較してみます。
ほとんどの月で、前月の営業回数が増加すれば今月の売上額も増加(前月の営業回数が減少すれば今月の売上額が減少)という傾向が見られました。
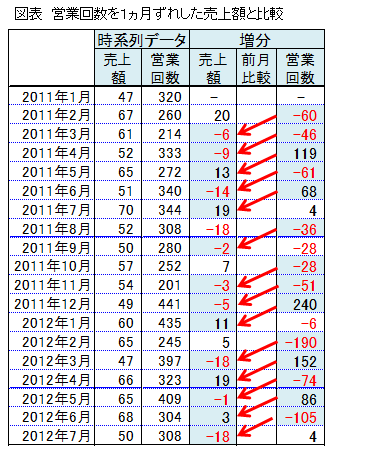
営業回数を1ヵ月ずらし、今月の売上額に合わせた時系列グラフを作成します。
このグラフから広告費の多い月は売上額も多いことがわかります。
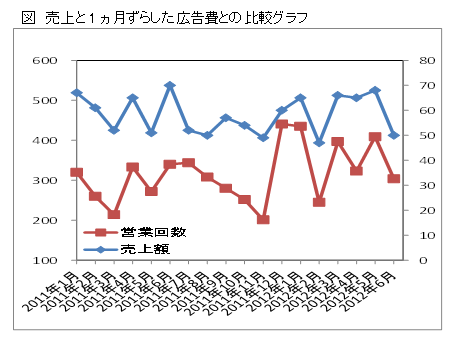
1ヵ月ずらしたデータで単相関係数、時系列相関係数を算出しました。これらの相関をタイムラグ単相関係数(タイムラグ相関と省略)、タイムラグ時系列相関係数(タイムラグ時系列相関と省略)と呼ぶことにします。
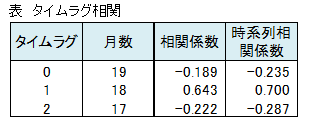
タイムラグ相関、タイムラグ時系列相関は下記に示すように0.2を上回りました。
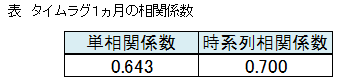
真の相関を表すタイムラグ時系列相関は0.7と高く、1ヵ月前の営業回数は今月の売上に大きな影響を及ぼし、売上額を予測する上で営業回数は重要な説明変数であることがわかりました。
この例題はタイムラグを1ヵ月で計算しましたが、もしかしたら2ヵ月前の営業回数が売上額に影響を及ぼしているかもしれないので、タイムラグは複数の月で計算しておくのがよいでしょう。
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。











