《数量化2類(3/3)》
2.数量化2類の応用/係数矛盾現象と説明変数の選択方法
係数矛盾現象が起こる例題
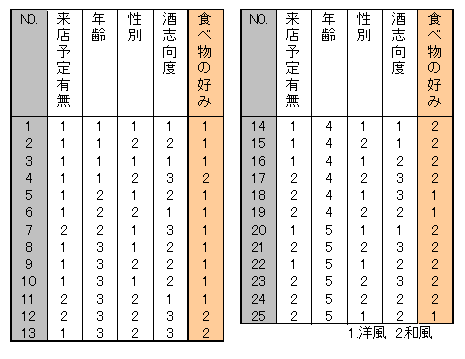
来店意向の説明変数に食べ物の好み(1.洋風、2.和風)を加え、説明変数を4つとしました。このデータに数量化2類を処理しました。
来店意向有りの人数を全体人数で割った横%が大きければカテゴリースコアも大きくなります。ところが食べ物の好みはこのような傾向がみられません。この傾向を調べる手法として単相関係数を用います。単相関係数が0.5未満の説明変数があるとき、係数矛盾現象が起こったといいます。
下記表で①横%と②カテゴリースコアとの単相関係数を示しました。食べ物の好みの相関は-1なので係数矛盾現象が起こったと判断します。
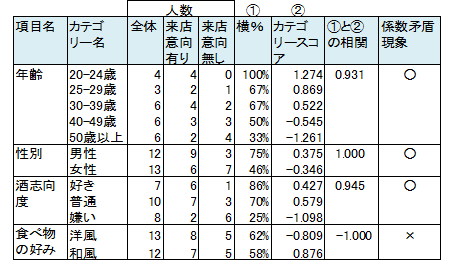
説明変数の選択方法
係数矛盾現象が起こらないカテゴリースコアを得るには、どのような説明変数を用いるかによって決まります。せっかく良いデータがあっても、説明変数の選択方法を知らないために、まずい関係式を算出している人がいます。ぜひ次に述べる事柄を理解し、素晴らしい関係式を求めてください。
目的変数と相関の高い変数を説明変数にします。相関は目的変数、説明変数どちらもカテゴリーデータなのでクラメール連関係数を用います。クラメール連関係数が0.25以上のものを説明変数にするのが一般的です。0.25という値は、必ずしも絶対的なものではなく、1つの目安です。先生の場合、0.1とかなり低い値を設定して、説明変数を多めにとり、次の方法で絞り込みを行っています。
ここで選ばれた説明変数の中から、次の方法によって説明変数の絞り込みを行います。
①説明変数相互で相関の高い変数を探し、どちらかの変数を落とします。
説明変数はカテゴリーデータなので、説明変数相互の相関はクラメー連関係数を用います。クラメール連関係数が0.5以上の2変数を探し、どちらかの変数を落とします。この値も上記同様に1つの目安です。落とし方は、落とす候補になった変数と目的変数との相関比をそれぞれ調べて、相関比の低い方を落とします。
下記の例では、X1とX2とのクラメール連関係数が高いので、どちらかを落とすことになります。 YとX1、YとX2のクラメール連関係数を比べるとYとX2の方が低いので、X2を落とします。

②データが全て同じ値の説明変数は落とします。
重回帰分析の解説ページ「説明変数の選択方法」を参照してください。
③カテゴリー別件数(n数)が2以下の説明変数は落とします。
説明変数ごとに、カテゴリー別件数(n数)を調べ、n数が2以下の説明変数は落とします。落としたくない場合、そのカテゴリーを他のカテゴリーへ統合するか、そのカテゴリーを削除して、数量化2類を実行します。
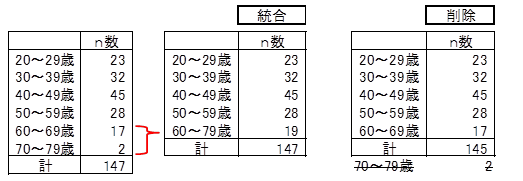
④将来設定ができない説明変数を落とします。
重回帰分析ページの「統計学的の理論的立場ではなく、分析者の判断から説明変数を選択」を参照ください。
係数矛盾現象が起こらないカテゴリースコア
来店意向データの説明変数の選択を行い、係数矛盾現象の起こらないカテゴリースコアを算出してみましょう。
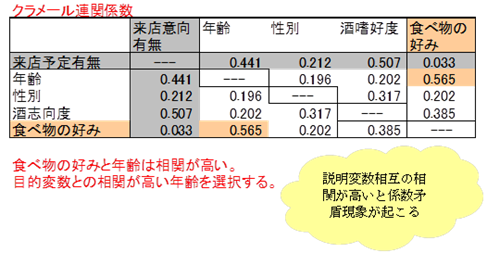
目的変数と説明変数とのクラメール連関係数を算出しました。食べ物の好みのクラメール連関係数は0.1を下回っているので、この項目は適用しません。
説明変数相互のクラメール連関係数(相関マトリックスという)を算出しました。クラメール連関係数が最大で0.5を上回った説明変数は、年齢と食べ物の好みです。来店意向有無と年齢のクラメール連関係数は0.441、来店意向有無と食べ物の好みとのクラメール連関係数は0.033なので、相関比の低い食べ物の好みを落とします。
予測
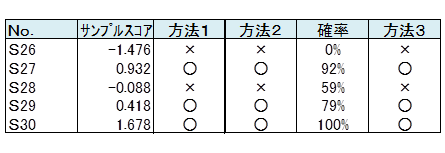
S26~S30の5名は来店意向がわからないと回答した人です。5人のサンプルスコアを算出します。サンプルスコアの値から、各人の来店意向の予測を行います。予測方法は3つあり、それぞれの方法を紹介します。
<方法1>
サンプルスコアがプラスなら来店意向があると判定します。この方法は簡便法で、次の方法2を推奨します。
<方法2>
判別的中点を求め、サンプルスコアが判別的中点より大きければ来店意向があると判定します。
<方法3>
サンプルスコアを来店意向確率に変換し、分析者が定めた基準確率、例えば75%以上の人を来店意向があると判定します。
3つの方法のよる結果を右に示します。
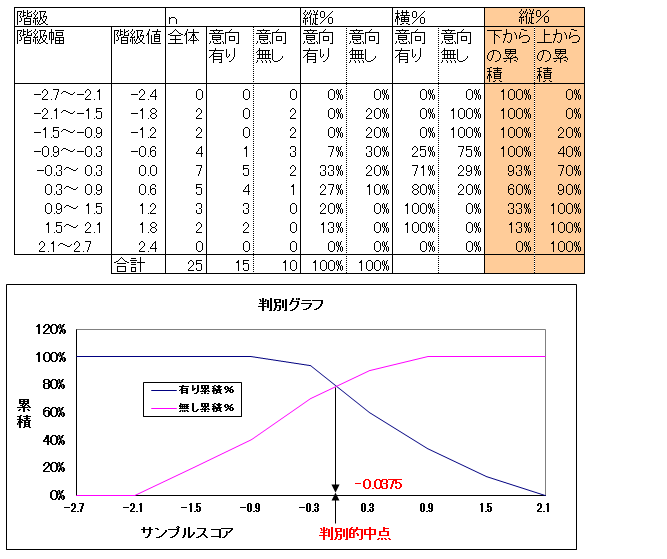
判別的中点
サンプルスコアの度数分布表を作成し、来店意向有り、来店意向無しの累積%グラフの交点の横軸の値を判別的中点といいます。
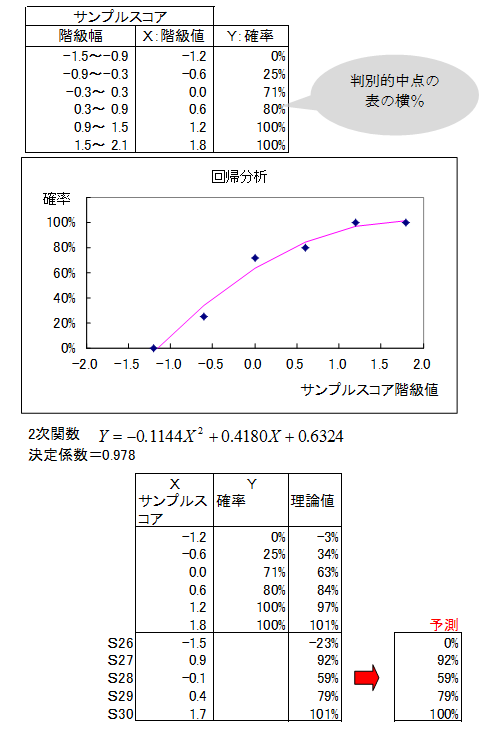
確率
判別的中点での横%を、当該階級幅に属するサンプルスコアの確率と判断します。
階級値と確率の散布図に2次関数を回帰分析によって当てはめます。
2次関数のXに予測する5人のサンプルスコアを代入し、確率を予測します。予測値がマイナスの場合は0%、100%を超えた場合は100%とします。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。











