

共分散と相関係数とは
データは20日分ありますが、簡単に計算できるように5日分のデータで説明します。
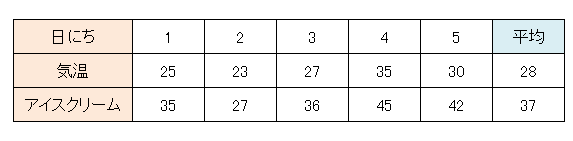
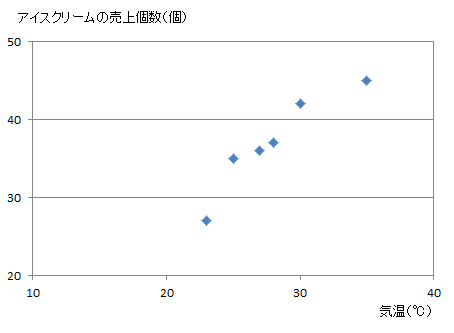
莉子:これは直線的傾向があるといってよさそうですね。
先生:そうだね。きっと2つの項目の関係は強いだろう。早速計算をしてみよう。
まずは日にちごとに、平均との差をとります。(=偏差)
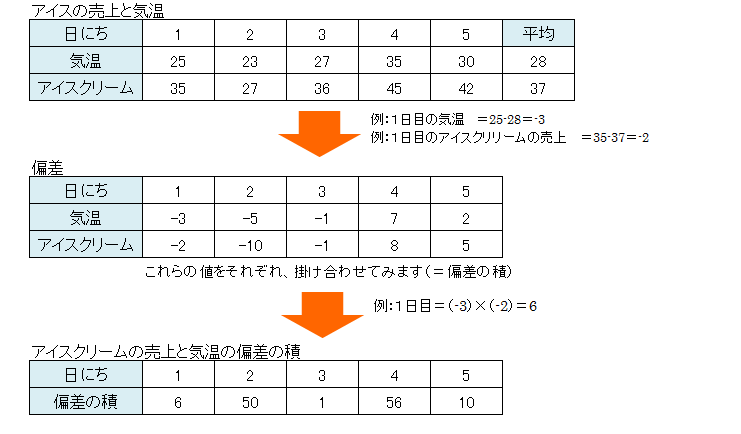
これらの値を合計(=偏差の積和)すると123になりました。偏差の積和は人数が多いほど大きい値になるので、人数に影響をうけないように、一人当たりの値を計算します。
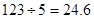
この値が共分散です。
先生:共分散が大きいほど2つの項目の関係が強いといえるんだ。
莉子:でも24.6は大きいのか小さいのか・・・・。
先生:そう。そこが共分散の弱点だ。共分散には上限がないから、24.6がどの程度の大きさなのかわからない。それにデータの桁数が大きいと、共分散の値も一緒に大きくなってしまうから、異なる単位や桁数が大きく異なるデータの共分散を比較することもできないんだよ。
莉子:それは不便だわ。何か良い方法はないですか。
先生:共分散をそれぞれの標準偏差で割れば、上限を1とした関係の強さを表すことができる。これが相関係数だよ。標準偏差は既に学習済みだから、僕が計算しておいた値を示そう。これを用いて相関係数を計算してごらん。相関係数の公式は次の通りだ。
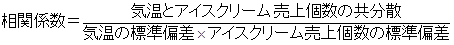

莉子:公式に値を代入すると0.94になりました。

先生:相関係数の上限は1だから0.94はかなり強い相関だということがわかるよね。
すぐに使える!!統計入門
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。









