
信頼区間、有意差検定、P値について学ぶ
第5話は、大学時代のゼミ仲間の田中君と卒業後偶然出会い、調査会社からのアンケート調査結果について相談された件がテーマである。
先週の日曜日、雪乃は大学時代のゼミ仲間の田中君と、卒業後2年ぶりに偶然出会いお茶した。雪乃が統計探偵事務所に勤めデータ分析の仕事をしていることを伝えると、田中君から「相談料は払えないけど教えて欲しいことがあるんだ。」といわれた。
田中君は月刊誌を出版している会社に勤めている。その月刊誌で主婦のへそくり金額の実態について掲載することになった。調査会社に調査から分析まで全面委託し、田中君が結果を要約し記事を書いた。記事にまとめたものの、統計学のことが分からず調査結果について雪乃に相談したいとのことだった。
田中君から後日、次の資料が送られてきた。
Wordファイル
・調査概要
・結果図
Excelファイル
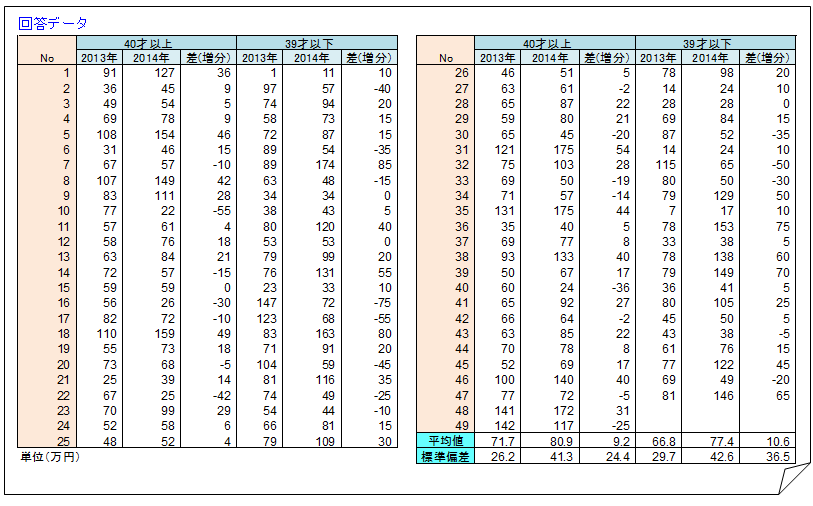
・アンケート調査回答データ
田中君は月刊誌を出版している会社に勤めている。その月刊誌で主婦のへそくり金額の実態について掲載することになった。調査会社に調査から分析まで全面委託し、田中君が結果を要約し記事を書いた。記事にまとめたものの、統計学のことが分からず調査結果について雪乃に相談したいとのことだった。
田中君から後日、次の資料が送られてきた。
Wordファイル
・調査概要
・結果図
Excelファイル
・アンケート調査回答データ
※Excelファイルは、以下の「Excel回答データ.zip」をクリックするとダウンロードできます。
(ファイルはzip形式に圧縮されています。ファイルを開くには、解凍ソフトが必要になります。)

田中君の疑問
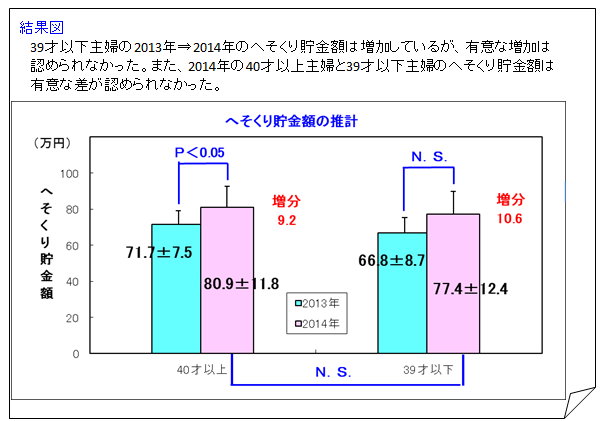
2013年⇒2014年のへそくり貯金額の増加について、39才以下主婦の方が増分が大きいのに、有意差は39才以下主婦で「ない」、40才以上主婦で「ある」という結果になっているのはなぜか。雪乃の対応
田中君の疑問を解決する前に、雪乃は「P<0.05」、「N.S.」、「±」は見たことはあるが、説明できる知識にいたっていなかった。そこで、所長にお願いし、レッスンしてもらうことになった。
レッスン内容
この図を理解するためには、次の①~⑩のレッスンが必要といわれた。
① 信頼区間とは何だろう
② 「±」とは何だろう
③ 信頼区間は幅が狭いほど推定の精度は良い
④ ヒゲとは何だろう
⑤ 「信頼区間」は○±△を図式化した以上の意味をもつ!
⑥ 標本誤差は主婦数とデータのバラツキから求められる
⑦ 母集団の平均値の違いを測るツール、それがP値
⑧ 「対応のある」、「対応のない」とは何だろう
⑨ 「対応のない」場合の有意差判定
⑩ 「対応のある」場合の有意差判定
ポイント ①:信頼区間とは何だろう
所長: 「2014年のアンケート調査において、40才以上主婦でへそくり貯金をしている人の人数と金額の平均値を教えて?」
雪乃: 「人数は49人、金額の平均値は80.9万円です。」
所長: 「ところで東京都に居住する40才以上主婦でへそくり貯金をしている人は何人ぐらいいると思う?」
雪乃: 「分かりませんけど、数十万人はいると思います。」
所長: 「アンケート調査の対象となった49人のデータで、数十万人はいると思われる40才以上主婦のへそくり貯金額平均値は80.9万円といってよいですか?」
雪乃: 「いえません。」
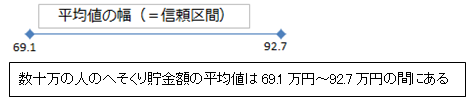
所長: 「そうだよね。だから、平均値はほぼこの範囲に収まるという幅を設定するんだ。具体的にいうと、40才以上主婦のへそくり貯金額の平均値69万円~93万円の範囲にあるというんだ。」
雪乃: 「範囲の値はどこから求めたのですか?」
所長: 「その幅の求め方が今回のテーマになるので、これから説明するよ。」
所長: 「ところで、母集団、標本という単語を知っているかな。」
雪乃: 「それくらいは知っています。この例でいえば、母集団は東京都に居住する40才以上主婦でへそくり貯金をしている全ての人。標本はアンケート調査の対象となった49人です。」
所長: 「OK。重要なので整理しておこう。」

所長: 「母集団全てのデータを集めることは難しく、統計は一部分のデータで全体の傾向を見なければならない。そこで統計学の考え方では、母集団からランダムに何人かを抽出して平均値を出すんだ。抽出作業を何回か行っても、平均値はほぼこの範囲に収まるという幅を設定する。」
雪乃: 「つまり先ほど教えてもらった69万円~93万円の中に何回行っても平均が収まるということですね。」
所長: 「『何回行っても』というのは正確ではない。一般に統計学の世界では100回行ったら5回くらいはその範囲に収まらなくても信頼性は十分という決まりがある。統計学では『69万円~93万円』を信頼区間(CI,Confidence Interval)という。」
雪乃: 「理解できました。」
所長: 「この例題の信頼区間を正確に計算すると次になるよ。」
ポイント②:「±」とは何だろう
平均値-標本誤差 平均値+標本誤差
所長: 「69.1万円~92.7万円はどうやってだすか考えてみましょう。49人のデータで、40才以上主婦のへそくり貯金額の平均値を求めると80.9万円です。ここで平均値に「いくつ」加えると92.7万円になるかな?
雪乃: 「92.7万円から平均値を引けばよいので、11.8万円です。
92.7万円-80.9万円=11.8万円
所長: 「平均値から「いくつ」引けば69.1万円になる?
雪乃: 「11.8万円です。
所長: 「統計学ではこの値を標本誤差(SE,Sampling Error)という。
標本誤差は統計学の公式によって求められるよ。後で公式を紹介するね。信頼区間は次の式によって求められる。平均値-標本誤差 平均値+標本誤差
この式をまとめて表記してみて。」
雪乃: 「平均値±
標本誤差」
所長: 「OK。40才主婦のへそくり貯金額について、この式で表記してください。」
雪乃: 「80.9±11.8(万円)です。これが上記の図に示されているんですね。」
所長: 「その通り。
【平均値±標本誤差】が表記されていれば信頼区間が把握できることは理解できたかな。」
雪乃: 「はい。」
所長: 「理解したかテストしてみよう。2014年の39才以下主婦の信頼区間を求めてみなさい。」
雪乃: 「上記の図をみると、2014年の39才以下主婦は77.4±12.4(万円)だから
77.4-12.4=65.0 77.4+12.4=89..8
2014年の39才以下主婦のへそくり貯金額は65.0万円から89.8万円の間にあるといえます。」
2014年の39才以下主婦のへそくり貯金額は65.0万円から89.8万円の間にあるといえます。」
所長: 「OK」
ポイント③:信頼区間は幅が狭いほど推定の精度は良い
所長: 「標本誤差(SE)が小さければ信頼区間はどうなると思う?」
雪乃: 「区間の幅が狭くなります。」
所長: 「区間の幅が狭いほど平均推定の精度が良いといえるんだ。」
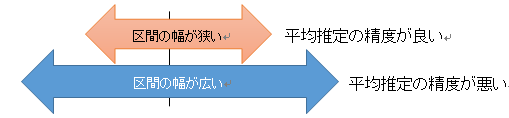
所長: 「Aの信頼区間は69万円から91万円、Bは31万円から131万円だったとする。どちらの方が平均値の推定は精度が良いかな。」
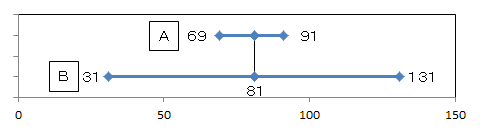
雪乃: 「Aです。」
所長: 「そうだね。Bの結果だと幅が広すぎて、へそくり貯金の推計は使いものにならないと思うよ。」
ポイント④:ヒゲとは何だろう
所長: 「右の図を見てください。棒グラフの上部からT字型の棒が出ているよね。これを『ヒゲ(error bar)』と言うんだ。ヒゲは何を表しているかな?」
雪乃: 「40才以上主婦の2014年のへそくり貯金額の80.9±11.8万円でいえば、11.8万円の値がヒゲです。」
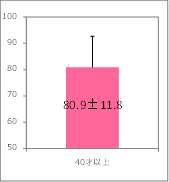
所長: 「その通り。標本誤差11.8万円をグラフの上に乗せて描いたときの線をヒゲという。また、この標本誤差の半分を標準誤差(SE,Standard Error)といい、標準誤差をヒゲとする描き方もある。今回のグラフは標本誤差を使っているよ。」
雪乃: 「ヒゲは平均値グラフの上だけでなく下にも描くと、推定される平均値の幅がわかりやすくなると思うのですが、どうして描いていないのですか?」
所長: 「それは棒グラフの中に納まって見にくいからだ。ただ、グラフによってはヒゲの下の部分も描いている場合もある。」
統計探偵物語
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










