信頼区間、有意差検定、P値について学ぶ
ポイント⑨：対応のない場合の有意差判定
所長： 「『対応のない場合』から説明しよう。
集団の平均値に着目して、母集団を調べることになる。今回のケースでいえば、40才以上主婦の2014年と39才以下主婦の2014年の平均値の違いを調べて、母集団の平均値の違いを評価することだ。」
集団の平均値に着目して、母集団を調べることになる。今回のケースでいえば、40才以上主婦の2014年と39才以下主婦の2014年の平均値の違いを調べて、母集団の平均値の違いを評価することだ。」
雪乃： 「先ほど、2014年において40才以上主婦と39才以下主婦の平均値は、それぞれの平均値の幅（＝信頼区間）を算出して比較すると教えてもらいましたけど、その方法ではいけないのですか。」
所長： 「その方法だよ。今までは『対応のない場合』を学んでいたんだ。
だから『対応のない場合』の説明はこれでおしまいにするが、今まで学んだことをまとめたまえ。」
だから『対応のない場合』の説明はこれでおしまいにするが、今まで学んだことをまとめたまえ。」
ポイント⑩：対応のある場合の有意差判定
所長： 「今から『対応のある場合』の説明をするよ。」
雪乃： 「よろしくお願いします。」
所長： 「『対応のある場合』は、その集団の平均値に着目しないんだ。今回のケースでいえば、40才以上（もしくは39才以下）の2013年の平均値と、2014年の平均値を比較してはいけないということ。右の表は雪乃の友人が持ってきた40才以上主婦のデータだ。差（増分）は、へそくり貯金額について2014年～2013年を引いた値だよ。」
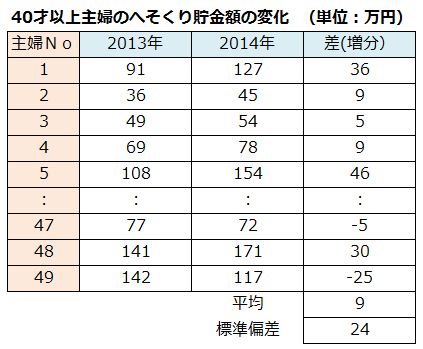
所長： 「『対応のある場合』では個々の人の差に着目するのが特色だ。主婦No1の差データはいくつかな？」
雪乃： 「36.0万円です。」
所長： 「『差データ』の49人分の平均値を計算してください。」
雪乃： 「36.0＋9.0＋5.0＋……（-5.0）＋30.5＋（-24.4））÷49＝9.2万円です。」
所長： 「次に、この『差データ』の信頼区間を計算してみよう。信頼区間を求めるには、まずは何を計算するのかな。」
雪乃： 「標本誤差です。」
所長： 「標本誤差の計算方法を覚えなくてもよいといったけど。ここでもう一度だけ使ってみよう。」
雪乃： 「計算してみます。標本誤差の公式を使います。」
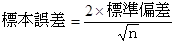
雪乃： 「田中君の持参データの末尾に記載されている『差データ』の標準偏差は24.4万円です。
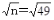＝7 標本誤差は2×24.4÷7＝7.0 です。信頼区間は平均±標本誤差 なので、『差データ』の信頼区間は9.2±7.0
これより2.2万円 ～ 16.2万円になります。」
0（ゼロ）を挟むということは+（プラス）も－（マイナス）もあるということだよ。
+（プラス）の場合は2014年が高くなり、－（マイナス）の場合は2013年が高くなる。」
雪乃： 「よく分かりません。」
所長： 「40才以上主婦の2013年と2014年の『差データ』の平均値の幅は2.2万円 ～ 16.2万円で0（ゼロ）を挟まない。ということは、別の40才以上主婦でも『差データ』の平均値はこの幅の範囲内となり、すなわち40才以上は39才以下を上回り、へそくり貯金額の増加が認められることになる。すなわち、母集団の2013年と2014年の平均値に違いがある、といえる。」
所長： 「一方で、『差データ』の平均値の幅に0（ゼロ）を挟んでいる場合は、別の主婦を調べたら『差データ』の平均値が+（プラス）になることも、－（マイナス）になることも、0（ゼロ）になることもある。
ということは、39才以下主婦の2013年と2014年でへそくり貯金額の増加が認められたり、認められなかったり、変わらなかったりするということであり、2013年と2014年で平均値に違いがあるかわからないということになる。すなわち、『母集団の平均値に違いがある、とは言えない』と判断する。」
雪乃： 「やっと分かりました。」
所長： 「39才以下主婦の2013年と2014年の『差データ』の平均値の幅（信頼区間）を計算してください。」
雪乃： 「公式を使います。」
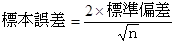
「田中君の持参データの末尾に記載されている『差データ』の平均値は10.6万円、標準偏差は36.5万円です。」
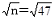＝6.86
「標本誤差は2×36.5÷6.86＝10.7 です。
信頼区間は平均±標本誤差 なので、『差データ』の信頼区間は10.6±10.7
これより －0.1万円 ～ 21.3万円になります。」
信頼区間は平均±標本誤差 なので、『差データ』の信頼区間は10.6±10.7
これより －0.1万円 ～ 21.3万円になります。」
所長： 「グラフを描いてみて。」
雪乃： 「了解です。」
所長： 「39才以下主婦の2013年と2014年では、母集団におけるへそくり貯金額の平均値に違いがありますか？」
雪乃： 「ありません。」
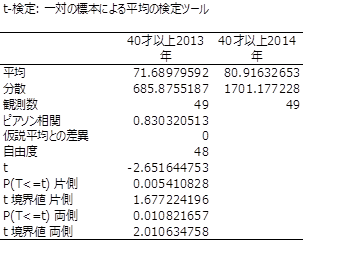
所長： 「『対応のある』場合でＰ値を求めてみると次になるんだ。」
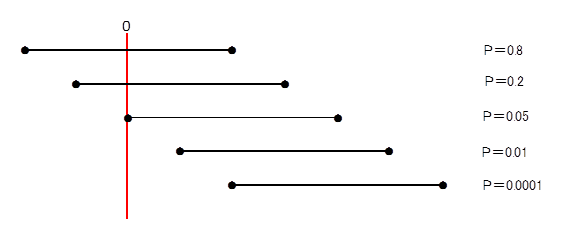
雪乃： 「分かりました。」
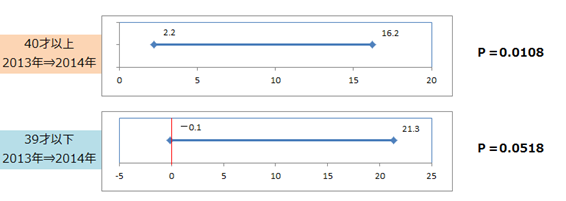
所長： 「ちなみに40才以上と39才以下の2013年⇒2014年のＰ値は次のとおりです。」
雪乃の田中君への回答
この回答を持って、後日、田中君と会った雪乃。
「2013年⇒2014年のへそくり貯金額の増加について、39才以下主婦の方が増分が大きいのに、有意差は39才以下主婦で「ない」、40才以上主婦で「ある」という結果になっているのはなぜか。」との疑問に対して、次の回答をしました。
40才以上の差データ、39才以下の差データの平均値を見ると、39才以下の増分が大きいです。しかし、40才以上の49人、39才以下の47人それぞれのデータのバラツキに着目すると、39才以下の方がデータのばらつき（標準偏差）が大きいです。
差データの標準偏差 40才以上→24.4 39才以下→36.5
統計学上の処理を行うと、40才以上のＰ値は0.0108、39才以下のＰ値は0.0518でした。
Ｐ値は平均値だけでなく、ｎ数やデータのバラツキも考慮して算出されます。
今回のデータでは、ｎ数は両群間に大きな差がないことから、このＰ値の差はデータのバラツキに起因すると考えられます。また、Ｐ値は一般的に0.05を下回れば「有意差あり」、上回れば「有意差なし」と判断しますので、39才以下主婦はわずかですが、統計学上では『有意差なし』となります。
田中： 「雪乃さん、すばらしい。ところで、40才以上より、39才以下で標準偏差が大きいということはどういう事なの。」
雪乃： 「それはですね。えーと、田中君の持参したデータを見て説明するね。各々最も小さい値と最も大きい値を探してみて。」
田中： 「40才以上 最小値 －55 最大値 54」
「39才以下 最小値 －75 最大値 85」
「39才以下 最小値 －75 最大値 85」
雪乃： 「39才以下主婦の方が2013年→2014年の変動が大きいということ。差データの平均値の推定は変動が大きい方がしにくい。だから有意差がある判定がしにくくなると思ってくれればいいわ。」
田中： 「説明もうまいなー。これから時間ある？ご馳走するよ。」
第5話 終わり
制作: 菅 民郎
理学博士
株式会社アイスタット代表
ビジジネス・ブレークスルー大学大学院 名誉教授
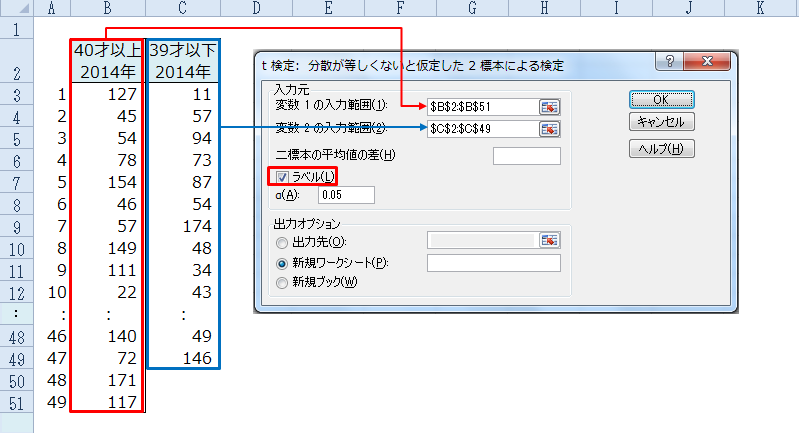
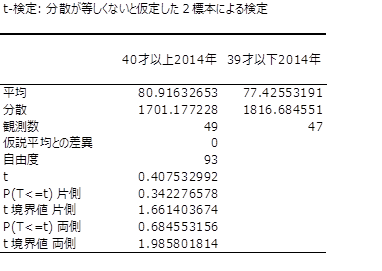
参考 Ｅｘｃｅｌの分析ツールを使って有意差を調べる
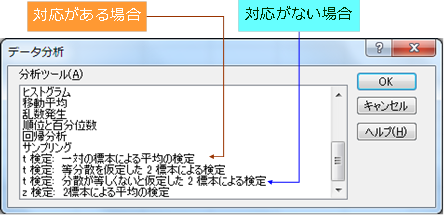
対応がある場合
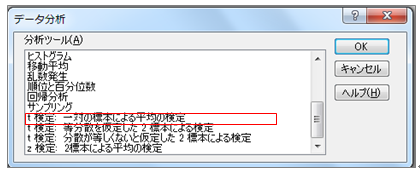
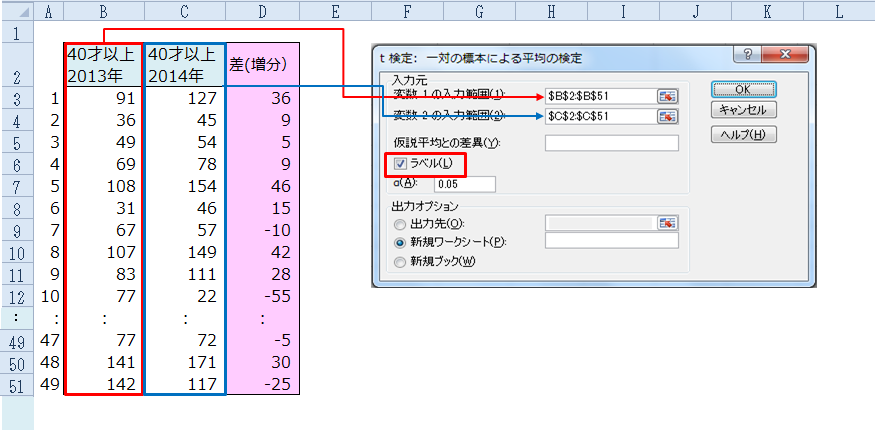
対応がない場合
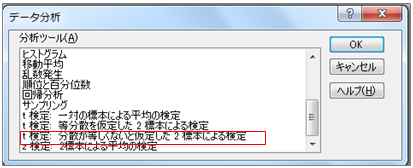
統計探偵物語
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング＆マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。
