信頼区間、有意差検定、P値について学ぶ
ポイント⑤:「信頼区間」は○±△を図式化した以上の意味をもつ!
所長: 「信頼区間は単に○±△を図式化したという以上の意味を持ちます。」
雪乃: 「どのようなことですか?」
所長: 「2014年における40才以上主婦と39才以下主婦のへそくり貯金額の信頼区間を並べてみてください。」
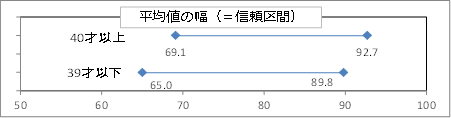
雪乃: 「40才以上主婦 69.1万円~92.7万円」
「39才以下主婦 65.0万円~89.8万円」
所長: 「これらを並べた図にしてください。」
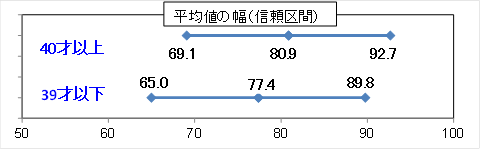
所長: 「40才以上の平均値が最も低くなるのはいくつ?」
雪乃: 「69.1万円です。」
所長: 「39才以下の平均値が最も高くなるのはいくつ?」
雪乃: 「89.8万円です。」
所長: 「この結果からどのようなことが言える?」
雪乃: 「そうですね、アンケート調査の結果は40才以上が80.9万円で39才の77.4万円より高くなっているのに、母集団における平均値は『40才以上が39才以下を下回る』ということがあるということですね。」
所長: 「そうだ。グラフを見ると、40才以上と39才以下で平均値の幅が重なっているところがあるだろう。このような場合、『母集団における40才以上と39才以下の平均値に違いがある』とは言えないんだ。次の場合、母集団の平均値に違いがあるといえますか?」
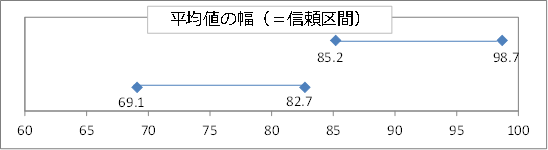
雪乃: 「平均値の幅が重なっていないので、違いがあると言えます。」
所長: 「その通り。」
雪乃: 「図(上記)から母集団の平均値に違いがあることはわかりましたが、この結論は100%正しいといえるのですか?」
所長: 「統計学は神様じゃないさ。外れることもあるよ。統計学から導かれる結論は当たる確率は95%、誤る確率は5%以下で信頼区間は求められている。」
ポイント⑥:標本誤差は主婦数とデータのバラツキから求められる
所長: 「データのバラツキを求める基本統計量は何?」
雪乃: 「馬鹿にしないください。その位知っています。標準偏差です。」
所長: 「雪乃の友人から入手したデータ表をみせてください。このデータ表の末尾に標準偏差は記載されているね。標本誤差は調査したデータの数(n)とデータのばらつき(標準偏差 SD, Standard Deviation)から決まります。nが大きいほど、ばらつきが小さいほど標本誤差は小さくなります。」
雪乃: 「とういことは、n数が大きくデータのばらつきが小さいほど、信頼区間の幅は狭くなり、精度が良くなるということですか?」
所長: 「その通り。」
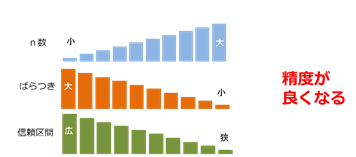
所長: 「具体的には標本誤差の計算式は下のようになります。」

所長: 「この式は覚える必要がないけど、この式の意味は理解しておくこと。」
雪乃: 「分子に標準偏差、分母にn数か。ということは、データのばらつき度合いが小さく、n数が大きいと、標本誤差は小さくなりますね。標本誤差が小さいということは、信頼区間の幅は狭くなり、精度が良いということですね!」
所長: 「その通り、下記表で標本誤差が最も小さいのは?」
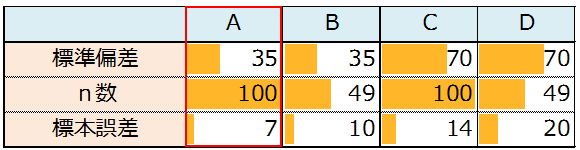
雪乃: 「Aです。」
ポイント⑦:母集団の平均値の違いを測るツール、それがP値
所長: 「実は、母集団の平均値に違いがある、もしくは違いがあるとはいえない、というのは『P値(Probability Value)』というものを用いてもわかる。というよりは、最近はP値で違いを表現することが主流です。P値は標準偏差などと同様に手計算すると手間がかかるけど、今はパソコンのソフトウエアで瞬時に出力できるんだ。」
雪乃: 「せっかく平均値の幅(=信頼区間)や、母集団の平均値に違いがあるかどうかを勉強したのに、無駄だったんですか?」
所長: 「少しも無駄ではないよ。P値は、2つの信頼区間の重なり具合によって決まる値なので、信頼区間とP値は同じものだよ。」
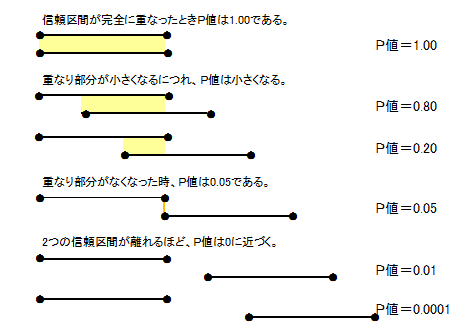
雪乃: 「よく分かりました。」
所長: 「P値が0.05より小さければ、信頼区間が重なっていないので、母集団の平均値に違いがあると判断する。
統計学では、P値<0.05の場合「有意差がある」という。
P値が0.05より大きければ、信頼区間が重なっているので、母集団の平均値に違いがあるといえない(有意差がない)と判断する。」
雪乃: 「2014年における40才以上と39才以下の信頼区間のP値を教えてください。」
所長はExcelを起動させあっという間にP値を算出した。
所長: 「P値は0.68です。これより40才以上と39才以下では有意差がないと判断する。」
雪乃: 「P値が理解できてうれしいです。」
所長: 「そんなに喜ばれたんだから、もう一つ付け加えよう。P値はよく、体をかがめてバーをくぐるリンボーダンスに例えられる。かがんだ高さがP値で、バーの高さが0.05なんだ。ということで、リンボーダンスのダンサー(求められたP値)がバー(0.05)を下回ればセーフで、母集団の平均値に違いがある(有意差がある)、と判断するのだ。」

雪乃: 「リンボーダンス知らないので、かえってわからないです。」
所長: 「そうなの、それは残念。」
雪乃: 「質問です。有意差は「P<0.05」でなく「P≦0.05」と定義している場合もありますがどちらの表記が正しいですか?」
所長: 「“≦”か“<”にあまりこだわる必要はない。」
雪乃: 「P値はどのようにして求めるのですか?」
所長: 「計算式が複雑なため手計算ではできません。ソフトウエアを使って求めます。後でExcelの分析ツールでの求め方を紹介しよう。」
雪乃: 「P値の0.05や0.016というのは、どういう意味なのでしょう?」
所長: 「P値が0.016ということは、母集団の平均値に違いがあるという結論がもしかしたら0.016、すなわち1.6%の確率で誤りになるということ。」
雪乃: 「ということは、P値が0.05だと5%の確率で誤りになるということですね。言い換えれば当たる確率は95%…、前回教えていただいた統計学の当たる確率95%と同じ数字ですね。」
所長: 「その通り! Pは「Probability」(=確率)の頭文字です。」
ポイント⑧:『対応のある』、『対応のない』とは何だろう
所長: 「『対応のある』とか『対応のない』とかを知っているかな?」
雪乃: 「聞いたことはあるけど意味は分かりません。」
所長: 「『『対応のある』というのは、今回のケースでいえば、40才以上主婦49人のへそくり貯金額の2013年と2014年の比較のことだ。要は、同じ人についての比較すること。」
雪乃: 「では、『対応のない』というのは何でしょう?」
所長: 「『対応のない』というのは、今回のケースでは、40才以上主婦の2014年へそくり貯金額と39才以下主婦の2014年へそくり貯金額を比較すること。異なる主婦群について比較することだよ。次を見るとよく分かるよ。」
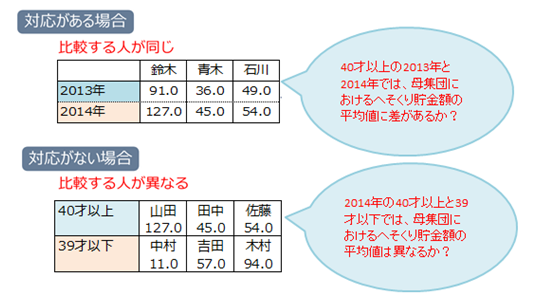
雪乃: 「先にある調査概要の調査目的①を解決するには『対応がある場合』、②を解決するには『対応がない場合』を適用するということですね。」
所長: 「その通り。『対応のある場合』と『対応のない場合』では、計算の仕方が違うよ。今からその違いを説明しよう。」
雪乃: 「何か難しそう。易しく教えてくださいね。」

統計探偵物語
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










