《数量化3類(2/3) 》
3.カテゴリースコア、サンプルスコアの求め方
カテゴリースコアの求め方
カテゴリースコアはどのようにして求められるかを調べてみましょう。
40代の男性10人を対象に、晩酌でよく飲むお酒の種類を日本酒、ビール、ウイスキーのなかから選んでもらうアンケート調査を行いました。
このデータ(下記イ)から、お酒とそれを飲む人の特性を分析し、回答のされ方が類似しているお酒、回答の仕方が類似している人を明らかにします。
アンケート調査の回答パターンから、お酒の種類と10人の男性両方に得点を与えます。その際、同じような特性をもつ人は同じようなお酒を好み、同じような特性のお酒は同じような特性をもつ人に好まれると仮定し、お酒と人とを得点化します。
このような得点は、次の考え方で求めることができます。
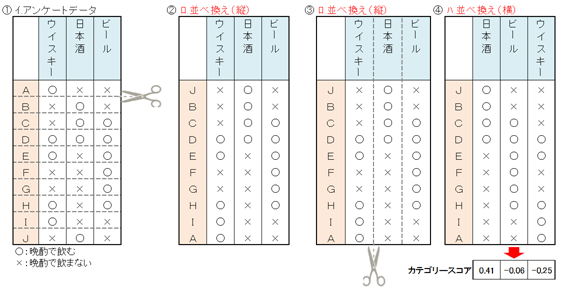
① 「イ」のデータを、横にはさみを入れてばらし、10枚の短冊を作ります。
② ○ができるだけとなりあうように10枚の短冊を並べ換えます。→「ロ」
③ 「ロ」のデータを、縦にはさみを入れてばらし、3枚の短冊を作ります。
④ ○ができるだけとなりあうように3枚の短冊を並べ換えます。→「ハ」
この結果、「お酒」についても、「人」についても似ているもの同士が並びます。例えば、ウイスキーはビールの隣に位置しているので、ウイスキーは日本酒よりビールに似ている、JとBは似ている、JとAは似ていないなどです。
お酒に対する得点は、「ハ」のお酒の並びに対応した得点を付ければよいことになります。左に位置するお酒ほど大きな得点を付けることにします。
日本酒とビール両方に○がある人はCとDの二人で、日本酒とビールの一致個数は2であるといいます。全ての組み合わせについて一致個数を調べます。
得点の付け方は、お酒の並びだけでなく、一致個数も考慮します。この結果お酒に対する得点は、日本酒0.41、ビール-0.06、ウイスキー-0.25になりました。具体的な計算方法は割愛します。
お酒についた得点がカテゴリースコアです。
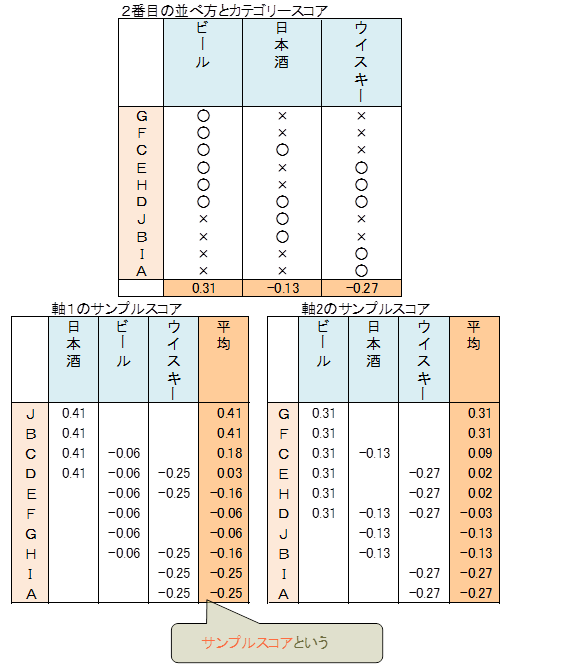
他の並べ方もたくさん考えられます。後ほど説明する、並べ方の良し悪しを調べる相関係数を用い、2つの並べ方を選びました。下記は2番目に良い並べ方とカテゴリースコアです。
1番目、2番目・・・を軸1、軸2、・・・と言います。
サンプルスコアの求め方
前記表で○のついたセルをカテゴリースコアに置換し、各サンプルの平均を求めます。平均の値をサンプルスコアと言います。
4.軸のネーミングとカテゴリー、サンプルのポジショニング
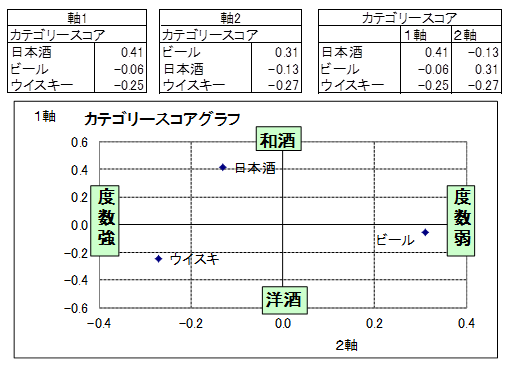
軸のネーミング
軸1のカテゴリースコアを縦軸、軸2のカテゴリースコアを横軸にとり、性格の散布図を作成します。
この図から、軸1の上側は日本酒、下側はウイスキーとビールなので、軸1は「和酒-洋酒」の判別軸と名称しました。
軸2の右側はビール、左側はウイスキーと日本酒なので、軸2は「アルコール度数強弱」の判別軸としました。
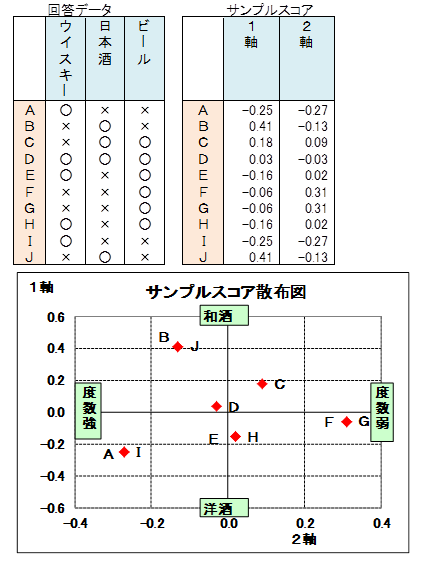
サンプルのポジショニング
軸1のサンプルスコアを縦軸、軸2のサンプルスコアを横軸にとり、各サンプルの散布図を作成します。
ネーミングされた軸で、各サンプルがどの位置に存在するか、また、どの人同士が近い位置に存在するかを把握します。
回答が同じ人は点の位置が重なっています。例えばBとJです。
上に位置するBとJは和酒(日本酒)、左下のAとIは度数が強い洋酒(ウイスキー)、FとGは度数の弱い酒(ビール)を晩酌でよく飲むお酒だといったことがわかります。
5.分析精度
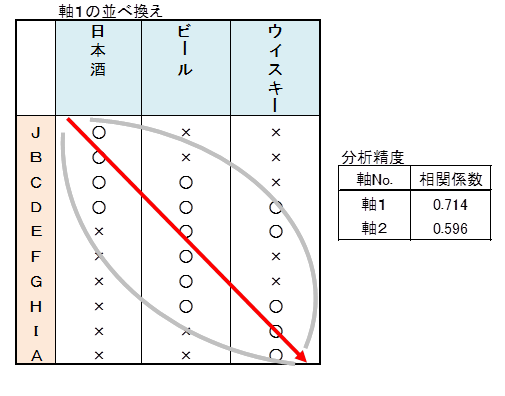
軸1の並べ換え表をみてください。いろいろな並べ換え表が存在しますが、下記の並べ換え表は、○の配置を囲む楕円形が最も細くなっています。楕円形が細い、言い換えれば赤線上に○の位置が近い並べ換え表ほど良いと判断します。並べ換えの良し悪しは下記で示す相関係数で求めることができます。
先生は、相関の高い軸を2~3個選んで分析します。ただし選んだ軸の相関係数は0.3以上あることを前提としています。
軸1について、並べ換え表の相関係数の求め方を調べてみます。
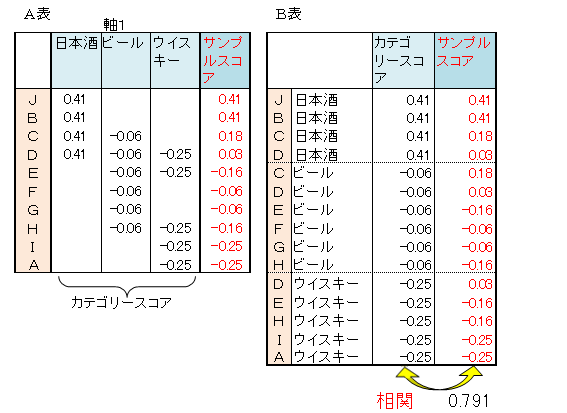
右の左側の表を再掲し、A表と名称します。
A表における日本酒を飲む4人のカテゴリースコアとサンプルスコアを、下記のB表の上段に記します。次にビールを飲む6人のデータを中段、ウイスキーを飲む5人のデータを下段に記します。
B表において、カテゴリースコアとサンプルスコアとの相関係数を算出します。相関係数は0.791となりました。
この相関係数の値が大きければ、並べ換え表は良いとされます。すなわち、その軸(潜在変数)は観察変数(この例では性格)を説明するのに重要だと判断します。
相関係数はいくつ以上あれば良いという統計学的基準はありませんが、先生は、相関が0.5以上の軸は説明力の高いと判断しています。そして、相関が0.3未満の軸は使わないことにしています。
コンピュータソフトにおいては、軸1、軸2は説明力の高い順に出力されいます。
数量化3類における固有値は相関係数の2乗のことです。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。









