数量化1類

HOME
>
多変量解析の手法別解説
>
数量化１類（１/３）

１　　２　　３　　次のページへ＞＞

《数量化1類（１/３）》

1.数量化1類の基本

数量化1類で明らかにできること

　数量化1類という手法は、「目的変数のある場合の手法」の一つで、重回帰分析と非常によく似た手法です。重回帰分析との違いは、説明変数のデータ形態が重回帰分析は数量データであるのに対し、数量化1類はカテゴリーデータであることです。

数量化1類は、目的変数と説明変数との関係を調べ、関係式を作成し、その関係式を用いて、次のことを明らかにする手法です。

①説明変数の各カテゴリーの目的変数に対する貢献度（影響度）

②説明変数の重要度ランキング

③予測

数量化1類で適用できるデータ

　数量化1類は、目的変数が数量データ、説明変数がカテゴリーデータです。

下記例題のデータ形態を調べてみます。目的変数は数量データですが説明変数はカテゴリーデータと数量データか混在しています。このままだと数量化1類は適用できません。年齢をカテゴリーデータにして、説明変数を全てカテゴリーデータにします。

数量化1類に適用するデータは次式の条件を満たしてなければなりません。

　個体数＞カテゴリー総数－説明変数個数＋１

　下記例題　：　９－３＋１＝７ → 個体数は８以上

この例題の個体数は200人なので、このデータは数量化1類が適用できます。

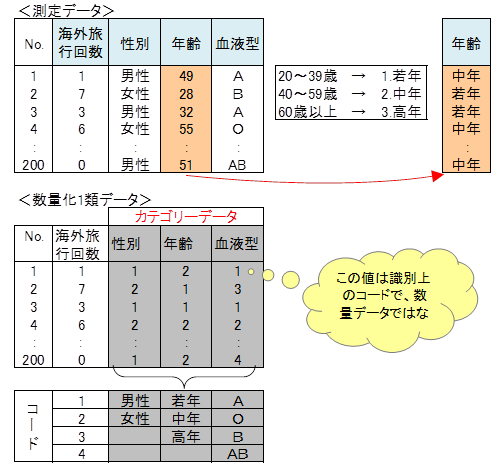
数量化1類の例題

　駅前の路上で朝の７時～９時の間、通勤者向けに新聞販売をしている店があります。ここで扱っているＡスポーツ新聞の売上部数を、店開きの１時間前までに予測し、その日の店に仕入れる最適な新聞部数（売れ残りや早い時間での売り切れがないような部数）を決めることにしましょう。

一般的に、スポーツ新聞の日々の売れ行きは、その日の曜日・天候・前日の巨人（野球チーム）の勝敗・当日および前後の日に競馬（ビッグレース）があるかどうかなどによって決まるようです。

そこで、野球シーズン中のある月の４週間にわたって、Ａスポーツ新聞の売上部数・天候・巨人の勝敗・競馬の有無を調べたところ、右の表の結果を得ました。

このデータを分析することにより、任意の日、例えば"月曜日で天候は小雨、前日の巨人の試合は中止、当日および前後の日の競馬がない"という日における、Ａスポーツ新聞の売上部数を予測します。

この例題に対する分析手順

この例題の分析手順を示します。

＜数量化1類を使う前の基本分析＞

①目的変数である新聞売上部数の基本統計量を算出

②説明変数ごとに、新聞売上部数のカテゴリー別平均値を算出
➡どのような日（曜日、天候など）において新聞は売れるかを把握

③新聞売上部数と説明変数との相関を算出
➡新聞の売れる・売れないに影響を及ぼしている説明変数を把握

＜数量化1類を適用しての分析＞

④予測するための関係式を作成

⑤関係式の係数矛盾現象をチェックする

⑥関係式の分析精度を調べる

⑦予測するための関係式を作成

数量化1類を使う前の基本分析

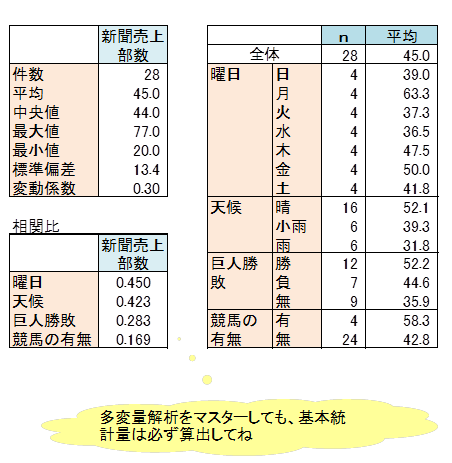
　２８日間の新聞売上部数の平均値は４５部です。

新聞売上部数のカテゴリー別平均値から、売れる日は月曜日、晴れ、巨人が勝つ、競馬がある日であることが分かりました。

相関比から新聞売上部数の売れ行きに影響を及ぼしている説明変数は、曜日、天候であることが分かりました。

カテゴリースコア

　カテゴリー別平均値から、「月曜日はよく売れるらしい」、「小雨の日はあまり売れないらしい」、また「前日に巨人の試合がなかった日や、当日または前後日に競馬がない日は売れないらしい」といったことが分かりました。残念ながら、この情報だけでは予測の問題は解決できません。そこで、カテゴリー別平均値から把握できたこと、すなわち各カテゴリーの新聞売上部数に対する貢献度を、何らかの方法を用いて数量で表現することを考えてみます。

具体的には、「月曜日は全体平均４５部より売上部数を７部多くするというプラス的働きがある」とか「小雨は平均売上部数を７部下げるというマイナス的働きがある」といった具合に、"月曜日"　"小雨"　というカテゴリーを数量化することを考えるのです。仮にすべてのカテゴリーに数量が与えられたとすれば、予測すべき新聞部数は、"月曜日"　"小雨"　"巨人の試合中止"　"競馬無し"　に与えられたそれぞれの数量（部数）と、平均売上部数との足し算によって導くことができます。

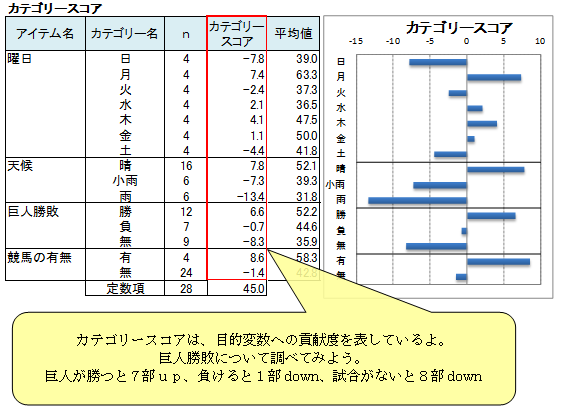
このような考え方で各カテゴリーの数量化を行う方法が、ここで学習する数量化１類という解析手法です。数量化された値のことを、数量化１類ではカテゴリースコアといいます。

新聞売上部数のデータに数量化１類を適用し、カテゴリースコアを求めると、次の表のようになります。