＜＜前のページへ　　　１　　２　　３　　４　　次のページへ＞＞

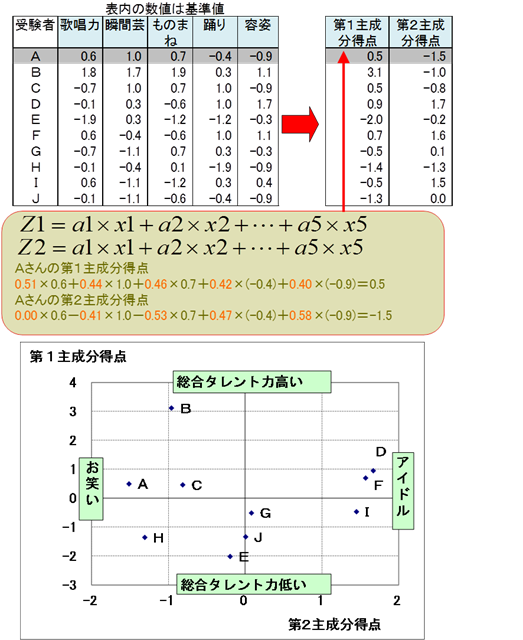
　下記は基準値データです。関係式に基準値を代入して求めた値を主成分得点といいます。

　縦軸を総合タレント力（第１主成分得点）、横軸を系別能力（第２主成分得点）として、散布図を作成しました。縦軸で０より上に位置するＡ、Ｂ、Ｃ、Ｄ、Ｆを合格としました。合格者のキャラクターは、横軸で０より右のＤ、Ｆをアイドル系、左のＢ、Ａ、Ｃをお笑い系としました。

　主成分分析を行い総合タレント力、系別能力の２つの主成分が見いだされましたが、もしかしたら３番目、４番目、･･･の主成分があるかもしれません。理論的には適用した変数の数だけ主成分は存在します。

　主成分分析の目的は、数多くある観測変数を数少ない潜在変数で説明することです。潜在変数は少ない方がよいのですが、少なすぎるとその潜在変数だけでは観測変数を説明できないかもしれません。一方、潜在変数が多すぎると観測変数に対する説明力は高まりますが、この例題のように受験者を２つの潜在変数である総合タレント力と系別能力の散布図に集約するといったことができなくなります。

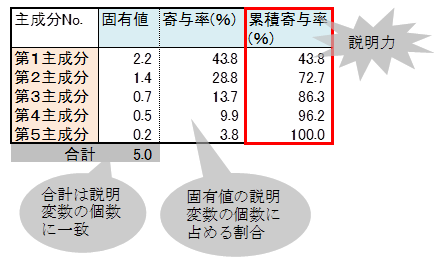
　主成分分析をパソコンソフトで行うと下記が出力されます。表内の累積寄与率が適用した潜在変数までの説明力を示しています。

　表内の固有値は各主成分の説明力で、合計すると観測変数の個数に一致します。主成分は固有値が大きい順に第１主成分、第２主成分、･･･、と名称します。寄与率は各固有値を観測変数の個数で割った値です。累積寄与率は当該主成分までの寄与率の合計です。

　主成分分析の潜在変数の個数は２～３がよいとされています。第２主成分まで適用した場合の説明力は７３％、第３主成分までの説明力は８６％です。説明力はいくつ以上あればよいという統計学的根拠はありませんが、先生は経験的に６０％ぐらいあればよいと思っています。そこでこの分析では２つの主成分（潜在変数）としました。

　潜在変数３つで説明力が６０％しかない場合、類似した説明変数を落として再度主成分分析を行います。落としたくない、落とせない場合は　潜在変数の数を増やさざるを得ません。

　　　

　目的変数のある場合の解析手法は決定係数、判別的中率など分析精度がありました。分析精度が高ければ目的変数の実績データと関係式から計算された理論値とは近く、この関係式は予測に使えると判断しました。目的変数のない場合の解析手法は、目的変数の実績データが存在しないので、関係式から計算された値（主成分分析では主成分得点）との突合せができず、分析精度はありません。

　分析精度に代る値が累積寄与率（説明力）です。

　主成分分析では複数個の主成分（潜在変数）を出力してくれますが、この例題の総合タレント力、系別能力という名称までは教えてくれません。この名称は分析者が決めなければなりません。

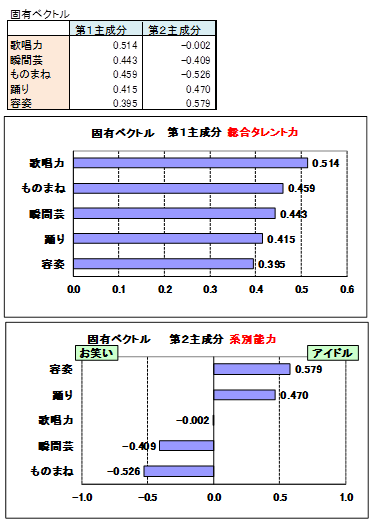
　主成分の名称は固有ベクトルの横棒グラフを解釈し決めるのが通常です。

　固有ベクトルが全てプラスの主成分は総合力を示します。大概の場合、総合力の主成分は一つで、第１主成分が総合力となります。

　固有ベクトルがプラスとマイナスが混在する主成分は相反する概念の能力を示します。この例題のアイドル系能力とお笑い系能力、学校のテスト成績における文系能力と理系能力、大相撲の体力測定のソッポとアンコなどです。

　この例題の第１主成分の固有ベクトルは全てプラスなので総合タレント力と名称しました。総合タレント力への影響度は、歌唱力、ものまね、瞬間芸、踊り、容姿の順となりました。

　第２主成分は容姿、踊りがプラス、ものまね、瞬間芸がマイナスで、前者をアイドル系能力、後者をお笑い系能力と名称しました。プラス、マイナスは相対的なもので符号が逆転していてもかまいません。

　主成分分析を実行したとき総合力が出力されないことがあります。このデータは主成分分析に適さないデータで、この後学習する因子分析を適用します。

　総合力が見出せないデータを紹介します。

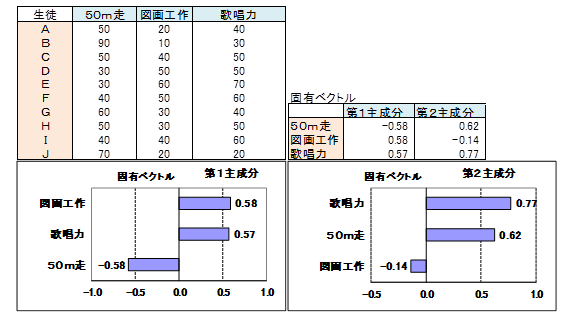
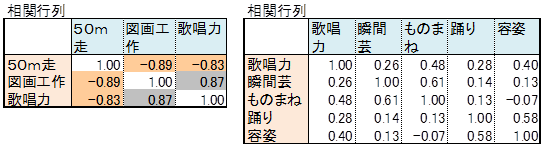
　次のデータは小学校６年生の１０人について、50ｍ走、図画工作、歌唱力を１００点満点で評価したものです。このデータに主成分分析を適用すると次表の固有ベクトルが導かれました。総合力は求められませんでした。なぜ導かれなかったのでしょうか。

　ここで観測変数相互の相関係数を算出してみます。相関係数はプラスで値が大きいもの、マイナスで絶対値が大きいものが混在しています。これに対しタレントの例題は説明相互の相関はほとんどプラスです。

　総合力が導かれなかったのは、説明変数相互の相関にプラスとマイナスがある、すなわち相反する概念のデータが存在したからです。

　相反するとは、50ｍ走の点が高い生徒は図画工作や歌唱力の点が低い傾向がみられるということです。

　３種目とも得点が高い生徒、逆に３種目とも点が低い生徒が多ければ総合力が導かれるのです。この例題のように全て良い生徒や全て悪い生徒がいない、すなわち片方が良ければ片方が悪いといったデータの場合は、総合力が導けないということです。導けないというより、導くことに意味がないといった方がよいかもしれません。

＜＜前のページへ　　　１　　２　　３　　４　　次のページへ＞＞