主成分分析
《主成分分析(1/4) 》
1.主成分分析の基本
主成分分析とはどのような解析手法か
多変量解析の手法は、目的変数がある場合とない場合の二つに分けられます。目的変数のない場合の手法は、説明変数が数量データの場合とカテゴリーデータの場合の二つに分けられます。説明変数が数量データの場合の手法は、主成分分析と因子分析があります。どちらの手法も、数多くの変数から新しい概念の変数を作ります。新しく作られた概念の変数を潜在変数といいます。これに対し、元の変数を観測変数といいます。
学校でのテスト成績を例にとると、通常、文系能力は国語と英語の合計、理系能力は数学と理科の合計で示します。しかし、国語や英語には文法問題、数学や理科には文書問題があり、「国語+英語」は文系能力、「数学+理科」は理系能力とは言い切れません。主成分分析は別の視点で文系能力、理系能力を見出す解析手法です。主成分分析より求められた文系・理系能力を潜在変数、単純に合計して求めた文系・理系得点を観測変数といいます。
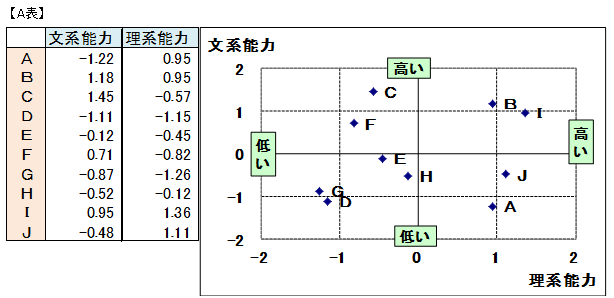
生徒の潜在変数における得点を計算し、右のAに示す散布図を作成します。この散布図から、文系能力の高い生徒は、C,B,I,理系能力の高い生徒は、I,B,J,Aであるといったこがわかります。
この散布図から、総合学力がある生徒、ない生徒を調べてみます。縦軸と横軸で大きな値を示したBとIが総合学力のある生徒、縦軸と横軸で小さな値を示したGとDが総合学力のない生徒と推察できます。
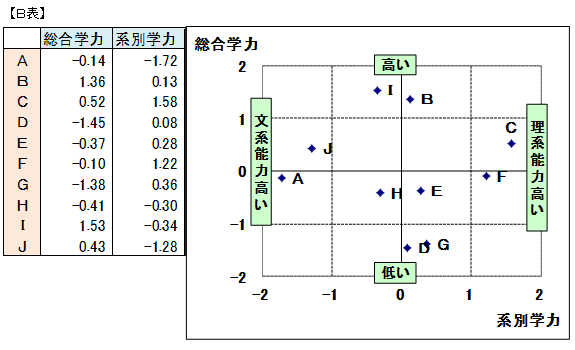
潜在変数を作成する際、最初から総合学力、そして文系能力と理系能力を判別する系別能力を作成することもできます。その結果をBに示します。この散布図から総合学力の高い生徒はIとB、低い生徒はGとD、理系能力が高い生徒はC,文系能力の高い生徒はAであるといったことがわかります。
AとBどちらにしても、英語、国語、数学、物理、化学の5つの観測変数を2つの潜在変数に集約し、一枚の散布図で10人の特色を明確に表しています。このすばらしい手法が因子分析と主成分分析で、Aの潜在変数を作成するのが因子分析、Bの潜在変数を作成するのが主成分分析です。
すなわち、潜在変数に総合学力、総合体力、総合企業力など総合力を見出したい場合は、主成分分析を適用します。
まず始めに、主成分分析について学びます。
主成分分析が適用できるテーマ
新人タレントを採用するために、芸能プロダクションはいろいろなオーディションを行っています。下記の表は、あるオーディションにおける受験者の歌唱力、瞬間芸、ものまね、踊り、容姿の成績(10点満点評価)を示したものです。
この成績から、各人のタレントとしての総合力、アイドル系・お笑い系の能力を把握し、採用の有無、採用後のキャラクター作りの決定を判断したいと思います。
このデータは説明変数だけで目的変数がありません。データは全て数量データです。分析を通し新しく見出す潜在変数に総合力があります。これらからこのテーマは、主成分分析の適用が最適だといえます。
主成分分析が適用できるデータ
目的変数がある場合の手法は、説明変数の個数より個体数が多くなければいけませんでしたが、主成分分析は説明変数の個数が個体数より多くても実行できます。
目的変数のない場合の手法で係数矛盾現象は起こりません。したがって説明変数相互の相関が高いデータでも問題ありません。
ある観測変数のデータが全て同じ場合、多変量解析同様実行できません。

主成分分析を適用する前の基本分析
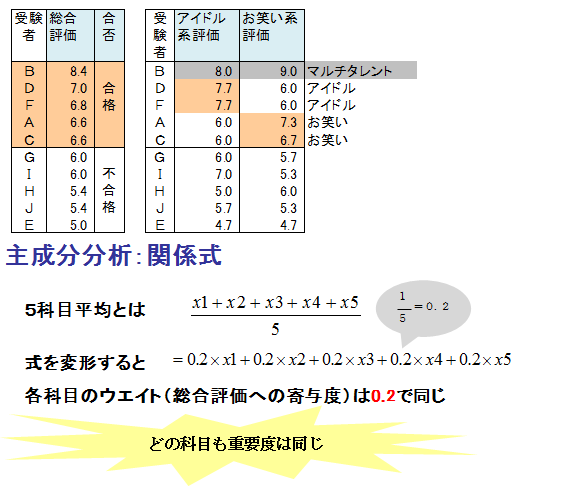
総合評価を調べるために、5科目の平均値を算出しました。5人採用とすれば、B,D,F,A,Cが合格です。
アイドル系能力は歌唱力、踊り、容姿の平均値で、お笑い系能力は歌唱力、瞬間芸、ものまねの平均値で調べました。歌唱力はアイドル系、お笑い系どちらにも重要な要素であると考え、両方の能力に適用しました。
Bはどちらの能力も優れているのでマルチタレント、DとFはアイドル系タレント、AとCはお笑い系タレントとして育成することにします。
ここで、5日科目平均値による総合評価について検討してみましょう。
ある生徒の5科目の得点を x1、 x2、 x3、 x4、 x5とし、その生徒の5科目平均値を式で示しました。変形した式の係数をみると、どの科目も0.2です。5科目平均値が総合評価だとしましたが、どのテスト科目も重要度は同じという考え方で総合評価を算出したということです。
関係式の係数
5科目平均値による総合評価は、どのテスト科目も重要度は同じという考えになっています。テスト科目の重要度を考慮して総合評価を算出するという考え方もあるはずです。
テスト科目の重要度を考慮した係数で関係式を作り、総合評価を求める手法が主成分分析です。
10点満点評価のデータに主成分分析を適用した結果をしめします。
目的変数のある場合の関係式は一つでしたが、目的変数のない場合は複数の関係式が導かれます。この例題では、総合タレント力と系別能力を求める2つの関係式が出力されました。
主成分分析では関係式の係数を固有ベクトルといいます。
「重回帰分析で関係式の係数である回帰係数の値を比較して、値が大きい説明変数は重要だとはいえない。その場合データを基準化して求めた係数(標準回帰係数)で比較すること。」ということを学びました。
主成分分析も同様です。特に主成分分析は説明変数の重要度を主目的とすることが多く、大概の場合基準化したデータで主成分分析を行います。
パソコン用ソフトで主成分分析を行う場合、生データ、基準値データのどちらで行うかを選択できます。ほとんどのソフトは、生データの主成分分析を「分散・共分散行列による主成分分析」、基準値を「相関行列による主成分分析」という用語を用いています。

統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。











