所長: 「他市の平均気温のデータがある。(図表17参照)この市の平均気温は上下変動して推移している。
このデータに直線回帰分析を行い、直線式、残差平方和を求め、平均気温の推移に直線を引く。
そして2015年、2020年の平均気温を予測するというテストだ。」

雪乃: 「できました。」
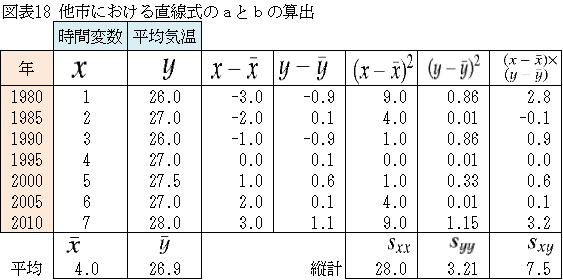
(図表18~22参照)
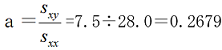
b=平均気温の平均 - a × 時間変数Xの平均
=26.9-0.2679×4.0
=25.86
直線式 Y=0.2679X+25.86


所長: 「よくできた、合格だ。」
雪乃: 「嬉しいです。」
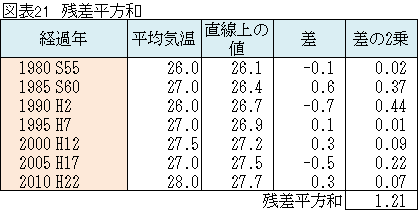
所長: 「残差平方和は1.21(図表21参照)で常夏市の残差平方和0.12に比べ大きいが、その理由は?」
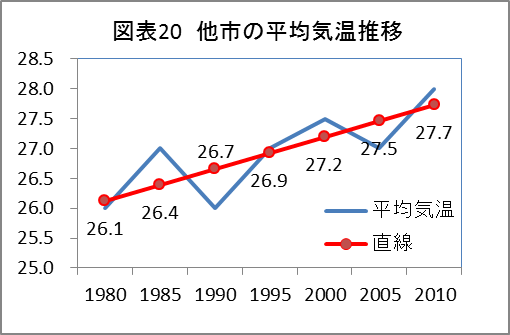
雪乃: 「他市の平均気温は上下に大きく変動して推移しているから、直線の当てはまりが悪いのだと思います。」
所長: 「そこでだ。残差平方和のSyy(平均気温の偏差平方和)に占める割合を計算すんだ。」
雪乃: 「常夏市について求めてみます。Syyは6.16、残差平方和は0.12だから、0.12÷6.16=0.02です。」
所長: 「他市は?」
雪乃: 「Syyは3.21、残差平方和1.21だから、1.21÷3.21=0.38です。」
所長: 「この値が小さいほど当てはまりが良いことは分かるよね。」
雪乃: 「はい」
所長: 「この値を定数1から引いた値が有名な決定係数なんだ。」
雪乃: 「ということは、常夏市の決定係数は1-0.02=0.98、他市の決定係数は1-0.38=0.62です。」
所長: 「OK」
雪乃: 「決定係数は大きいほど当てはまりが良いということですね。」
所長: 「そうだ。決定係数が大きければ2015年、2020年の平均気温予測値は信頼できる数値と考える。」
雪乃: 「決定係数が低いということを私なりに考えてみました。平均気温の推移に直線を当てはめてみたものの、上下変動が大きく推移しているので、『将来の平均気温は求められた直線上にあるといいきるのは危険』である。」
所長: 「なかなかいいじゃないか。素晴らしい。」
雪乃: 「決定係数はいくつ以上あれば良いという基準はありますか。」
所長: 「統計学的基準はないが、私の経験として0.5以下だと導かれた直線の式は予測には適用できないと思う。」
雪乃: 「常夏市の直線式の決定係数は0.98なので、予測値の精度は高いということですね。」
所長: 「その通り。」
雪乃: 「Excelで直線式を求める機能はありますか。」
所長: 「あるよ。」
雪乃: 「教えてください。」
所長: 「2つの方法があるので、まずは1つ目を教えよう。」
統計探偵物語
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。









