リスク比とオッズ比
◆リスク比とオッズ比(4/4)◆
4. ”後ろ向き研究”で使える手法はオッズ比のみ!
コホート研究とケースコントロール研究を知る!
前回までの説明で、オッズ比について何となくわかっていただけたと思います。しかし、リスク比のほうが使い勝手が良いように思われた方も多いのではないでしょうか?
では、なぜオッズ比が臨床研究で使われるのかというと、それなりにオッズ比の活用法があるからです。
代表的な臨床研究として、「コホート研究」と「ケースコントロール(症例対照)研究」がありますが、後者の研究で集めたデータを解析する場合、リスク比は不可、オッズ比は可だといわれています。
このことを説明する前に、「コホート研究」と「ケースコントロール研究」とは何かを簡単に説明しておきましょう。
臨床研究では「前向き」か「後ろ向き」か、で分けることができ、コホート研究は前向きの研究、ケースコントロール研究は後ろ向きの研究とされています。
具体例で説明していきましょう。喫煙の有無と不整脈の有無の関連性を調べたいとします。
1)コホート研究
不整脈がない人をランダムに400人抽出し、今までに喫煙をしたことがあるかどうかを調査し、その後の2年間において、喫煙の有無別に不整脈が発生したかを追跡調査します。調査開始時点では不整脈は発生しておらず、それから2年後(未来)に不整脈の発生を調べます。
このような研究をコホート研究といいます。この研究は2年後の未来へ向かって調べる研究であり、「前向き」の研究といいます。
2)ケースコントロール研究
不整脈があると診断された200 人とランダムに選んだ健常者200 人について、過去の喫煙の有無を調査します。すでに不整脈があると診断された人と健常者がいて、その時点から過去にさかのぼって喫煙をしていたかどうかを調べます。
このような研究をケースコントロール研究といいます。この研究は過去へ向かって調べる研究であり、「後ろ向き」の研究といいます。
この2つの研究の違いを、原因と結果という因果関係からみてみましょう。上記の例では、喫煙の有無が原因変数で不整脈が結果変数です。コホート研究は、未来の結果変数(不整脈の有無)を調べる研究であり、ケースコントロール研究は過去の原因変数(喫煙の有無)を調べる研究となります。
それでは、ケースコントロール研究で集めたデータを解析する場合、リスク比は不可、オッズ比は可だということについて説明します。
ケースコントロール研究でオッズ比が使われる!
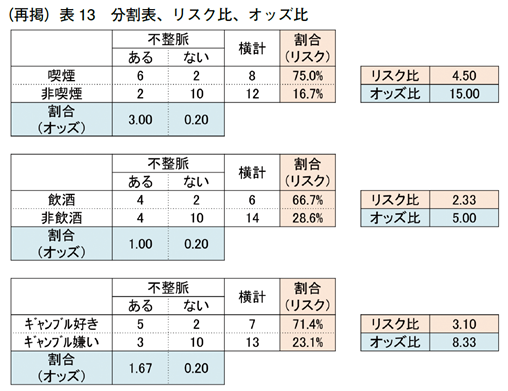
次のデータをケースコントロール研究(後ろ向き研究)で集めたデータということにします。

この分割表から、喫煙者が不整脈になるリスクは56%です。この数値から、一般的に喫煙する人が不整脈となるリスクが5割を超えているといってもよいでしょうか?
この事例はケースコントロール研究で集めたデータという設定です。不整脈があると診断された200 人とランダムに選んだ健常人者200 人について、過去の喫煙の有無を調査したものです。
したがって、全対象者における不整脈のリスク(割合)は200÷400 の50%で、調査対象者のサンプリング(抽出)に依存します。サンプリングに依存しているリスクを用いてリスク比を計算するのは、大きな間違いとなります。
ただし、リスク比の値を順位で検討するだけであれば、リスク比を使用しても構いません。しかしながら、この制限の下にリスク比を使うのなら、最初からオッズ比を使えばよいということになります。このような理由から、ケースコントロール研究の場合は、オッズ比を用います。
ロジスティック回帰分析とは
ケースコントロール研究ではオッズ比を用いることを学習しました。さらにもう1つ、知っておいてもらいたい「ロジスティック回帰分析」について、説明していきます。
下表12 をご覧ください。結果に対していくつかの原因が考えられる場合、それぞれの原因が、結果にどの程度影響を及ぼしていると思いますか?
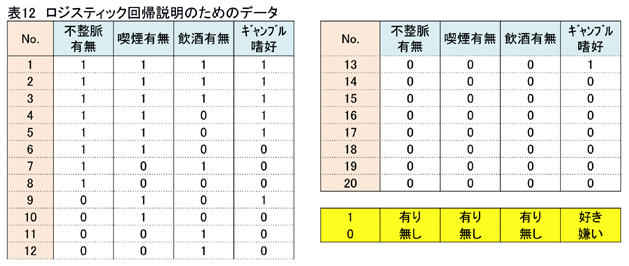
一目見ただけでは、なかなかわからないですね。
このデータでは、結果は「不整脈の有無」、原因は「喫煙」「飲酒」「ギャンブル嗜好」の3つを想定しています。今までの学習を思い出して、少し面倒ですが、このデータの分割表、オッズ比、リスク比を求めてみましょう。
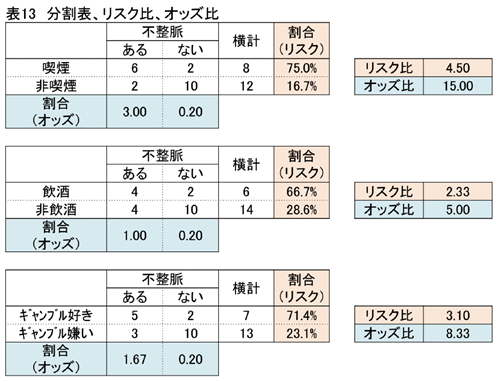
では、結果を解釈していきましょう。
結果をみるかぎり、不整脈に影響度の最も強いのは喫煙の有無、次にギャンブル嗜好です。飲酒の有無は3番目でした。ギャンブル嗜好のほうが飲酒の有無より影響度が高いのは、何かおかしな気がしませんか?
この結果が事実かどうかは、喫煙の有無、ギャンブル嗜好、飲酒の有無のそれぞれの原因の関係をみればわかります。つまり、不整脈という結果に対する原因がいくつか考えられる、ということです。これは「不整脈を説明する変数がいくつかある」ということと同じです。では、原因同士の関係性を調べてみましょう。
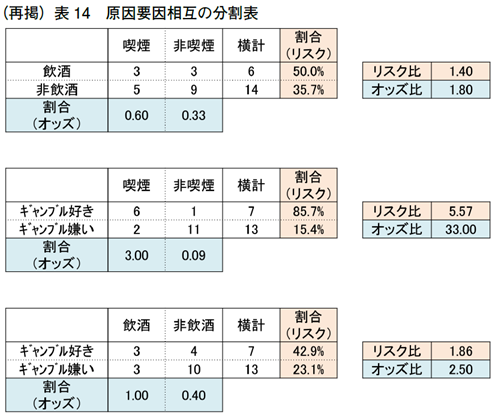
まず、「原因要因(影響要因)相互の分割表」というものを作成し、リスク比を求めていきます。飲酒の有無と喫煙の有無、ギャンブル嗜好と喫煙の有無、ギャンブル嗜好と飲酒有無で、原因要因相互の分割表を作ってみます。
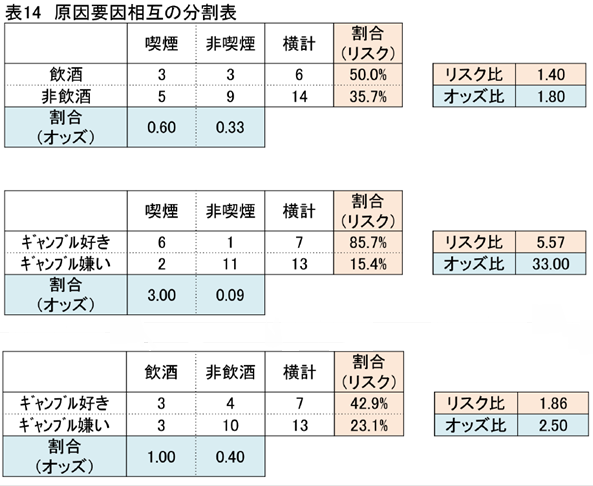
このように飲酒と喫煙、ギャンブルと喫煙、ギャンブルと飲酒のそれぞれの関係性や影響度合いをみていきます。上の表14 の結果をみて、どのようなことがいえるでしょうか?
ギャンブル好きは7人中6人が喫煙者、ギャンブル嫌いは13 人中11 人が非喫煙者です。リスク比も5.57と高く、両者に強い関係性を感じます。飲酒の有無と喫煙の有無のリスク比は1.40、ギャンブル嗜好と飲酒の有無のリスク比は1.86とそれほど大きな値でなく、関係性は弱いようです。
感覚的には、リスク比5.57というと強い関係性があるようにみえますが、結論から言えば評価する際の統計学的な基準はありません。言い換えれば、「リスク比がいくつ以上の値だから、強い相関がある」ということはありませんが、リスク比同士を比較して、“強い”“弱い”と評価をすることはできるということです。
では表13と表14 を基に、リスク比で、原因2つと結果(不整脈の有無)の関係をみてみましょう。喫煙の有無とギャンブル嗜好を原因にして、図式化してみます。
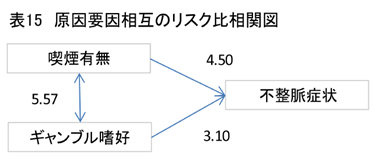
原因要因相互の関係で「強い相関はない」⇒ロジスティック回帰分析の必要なし!
ロジスティック回帰の計算は複雑なので、残念ながらExcelではできません。計算方法は、別の機会にするとして、アイスタットソフトウェア「マルチ多変量」で解いてみましょう。
(※ ソフトウエアはアイスタット社から1ヵ月間、無料貸出します。)
「マルチ多変量」で解析した結果を表16に示します。
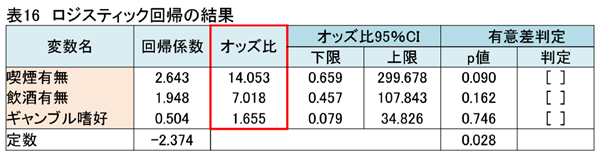
このようにロジスティック回帰を行うと、オッズ比が出力されます。オッズ比から順位が把握できるので、不整脈の原因要因の1位は喫煙の有無で、次に飲酒の有無となります。ギャンブル嗜好は、不整脈にそれほど影響がないことがわかります。
つまり、表16 の結果と表13 の結果が異なるということは、原因要因が多数あるときは、ロジスティック回帰を使わなければいけないということです。
原因要因が相互に無関係と解釈できれば、分割表のオッズ比とロジスティック回帰のオッズ比の順位は同じになります。したがって、表14 で示した原因要因相互の分析をして強い相関がないことがわかれば、ロジスティック回帰分析をする必要はありません。
ここで、表16 のp値について説明しておきます。
p値が0.05 以下であれば、今回のサンプル20 人から、何十万人という母集団についても、その原因は不整脈に影響を及ぼすと判断されます。表16 は、3要因ともp値は0.05 以上なので、母集団においてこれら3要因が原因であるかどうかはわからないということです。
オッズ比が14.053 とかなり大きいのに、p値は0.05 を下回らないのは不思議な感じがしますね。それはサンプルが25 人と少ないからでしょう。統計学の解析手法では、少ないサンプルからは有意差判定ができないと判断したのです。
ロジスティック回帰については、ここでは「原因要因相互の関係を考慮してオッズ比を算出する解析手法」くらいに理解しておいていただければよしとしてください。
ところで、分割表から求められたリスク比から、母集団についても影響がある/ないということをいえると思いますか?
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。











