リスク比とオッズ比
◆リスク比とオッズ比(2/4)◆
2. よくあるオッズ比の間違った解釈
はじめに簡単な事例で、オッズ比を勉強していきましょう。
オッズは、競馬など賭け事でよく使われますので、勝負事の例で解説していきましょう。たとえば、スマホやパソコンにあるゲームを何でも良いので、5セットを1回として計2回やったとします。
下記の表5は1回目と2回目のゲームの勝敗の成績を示したものです。
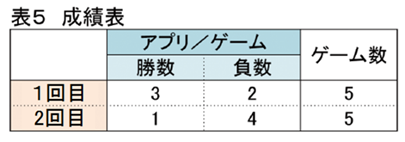
ゲームの勝敗の成績を、仮に、「1.分割表とリスク比」で学んだ喫煙の有無と不整脈の有無との関係と同じ結果になるようにしました。
では、オッズの説明をする前にリスク比について、もう一度おさらいしておきましょう。この表5についてリスク比を求めて、リスク比から何がいえるかを考えてみます。
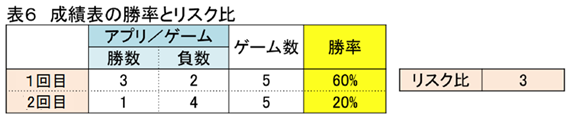
1回目の勝率は60%、2回目の勝率は20%、勝率の比、すなわちリスク比は、60%÷20%により3となります。リスク比から、1回目の勝率は2回目に比べ3倍であり、勝率をゲームの強さと考えると、1回目のゲームの強さは2回目に比べ3倍強いといえます。
それでは、この成績表を用いてオッズ比について説明していきます。
まず、1回目の勝数を2回目の勝数で割った値を「オッズ(Odds)」といいます。
そして、1回目の負数を2回目の負数で割った値もオッズといいます。
どちらもオッズというので混乱しそうになりますね。
もう少し説明を続けます。
勝数に着目すると、1回目の勝数(3勝)は2回目(1勝)に比べ3倍、すなわち、勝数オッズは3です。
負数に着目すると、1回目の負数(2敗)は2回目(4敗)に比べ半分、すなわち、負数オッズは0.5となります。
そして、ここからが大切なところですが、勝数オッズと負数オッズの比を「オッズ比(Odds Ratio)」というのです。
それぞれを、勝数オッズと負数オッズと言い、オッズ比は3÷0.5で算出しますので、6となります。
では、このオッズ比から、1回目の勝率が2回目に比べ6倍、1回目のゲームの強さは2回目より6倍だといってよいでしょうか?
答えは間違い! 絶対ダメです。大間違いとなります!
ここが、多くの方が陥るオッズ比の典型的な間違った解釈です。勝率(強さ)の比較は、リスク比でしかできないのです。
では、オッズ比から何がわかるのでしょうか。
実は、オッズ比の値が大きいとか、小さいといったことがわかるだけなのです。だからオッズ比は、リスク比に比べ理解しにくく、そのため使い方に注意がとても必要となるのです。
オッズ比でわかるのは影響要因かどうかということ
喫煙の有無と不整脈の有無の事例の分割表(表3、1.分割表とリスク比で掲載)を用い、これについてリスク比とオッズ比を求めて、解釈してみましょう。
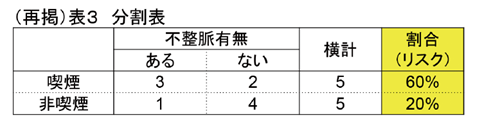
リスク比とオッズ比を、下表にまとめてみました。

喫煙者の不整脈のリスクが60%、非喫煙者の不整脈のリスクは20%、リスク比は60%÷ 20%で3となります。
ですから、喫煙者が不整脈となるリスクは非喫煙者に比べ3倍であるといえます。
次に、オッズ比を計算してみましょう。
不整脈があるケースのオッズは、喫煙者が3、非喫煙者が1ですから、3÷1からオッズは3。
不整脈がないケースのオッズは、喫煙者が2、非喫煙者が4のため、2÷4からオッズは0.5。
これより、オッズ比は3÷0.5 で6となります。
オッズ比の値は6と大きいので喫煙の有無は、不整脈の影響要因といえそうですが、絶対に間違ってはいけないのは、「喫煙者が不整脈となるリスクは非喫煙者に比べ6倍だと言ってはいけない!」ということです。
このように解説していくと、オッズ比はリスク比と比べるとあまり使い道がないように思われるかもしれません。しかし、実際の臨床研究の論文では、オッズ比はよく使われています。このように理解しにくいオッズ比がなぜ、臨床研究で使われているのか。それはそれなりに、オッズ比の活用法があるからということです。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。









