分散分析法・F検定
◆分散分析法・F検定(1/2)◆
適用できるデータ
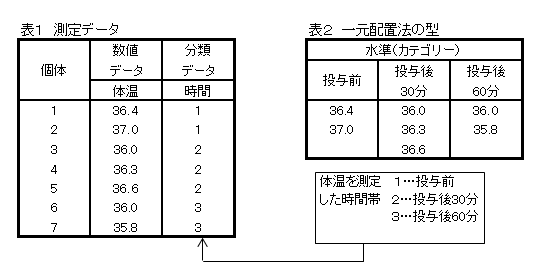
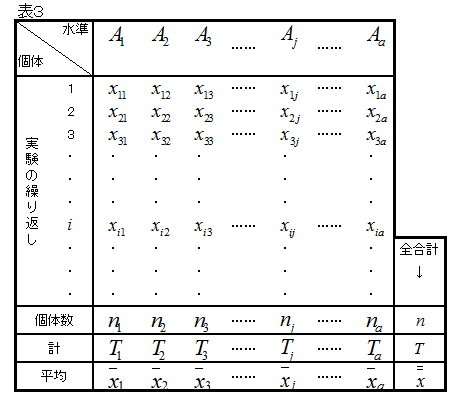
表1は、7人について体温、測定した時間帯を調査したものです。
この表におけるデータを並べ替えたものが、表2です。表2の型で整理した表のことを一元配置法の型といいます。
実験計画法では、目的となる数量項目(この例では体温)を「特性値」あるいは「計量値」といい、分類の項目を因子(この例では体温を測定した時間帯)といいます。また、分類項目のカテゴリーを、(因子の)水準といいます。

下の表は、一元配置の一般的な型を示したものです。

分散分析法とは
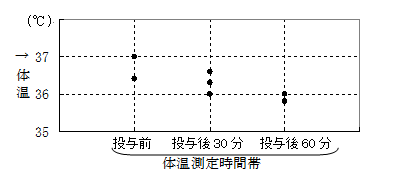
表2の一元配置で得られたデータについて考えてみましょう。このデータをグラフで表すと、右図になります。
この図から明らかなように時間帯が変わると、体温は変化します。しか
し、同じ時間帯でも体温が一定になるのではなく、たとえば、投与後30分では最低36.0度から最高36.6度までばらついています。
すなわち、表2で示されたデータ全体のばらつきの中には、
①測定時間の水準を変えたことによるばらつき
②同じ測定時間帯のもとで実験を繰り返したときに起こるばらつき
とが、混合していることがわかります。
この実験全体の持っているばらつきを全体変動、①におけるばらつきの部分を因子間変動(級間変動)、②におけるばらつきを誤差変動(級内変動)といいます。
ここでもし、測定時間帯の水準を変えたことによって、データのばらつきが大きくなったとすれば、因子間変動と誤差変動の割合は図aのように因子間変動が大きくなり、時間帯を変えてもばらつきが大きくならなければ、図bのように因子間変動の割合は小さくなります。
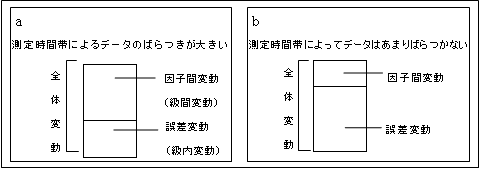
図a、bから明らかなように、因子間変動の割合が大きければ、因子の水準を変えたことによって効果があったと考えます。従って因子の効果は、因子間変動と誤差変動の比較によって決まります。一般的に、因子の効果を主効果といいます。
このように、データの持っている変動を、因子や誤差の変動に分けて、因子による効果を調べる方法を分散分析法といいます。分散分析法は実験計画法だけでなく、あらゆる統計解析手法に連動して適用されている手法です。
「変動」の分解の考え方
統計学的にデータの持っている全体変動を、因子や誤差の変動に分けることを「変動の分解」といいます。
どのような方法で変動を分解するか、考えてみましょう。
全体変動をS とすると、S は個々のデータと総平均との差の平方和ですから、次の計算式で表せます。
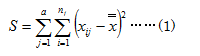


表2のデータを用いて、(4)式が成立することを確かめてみましょう。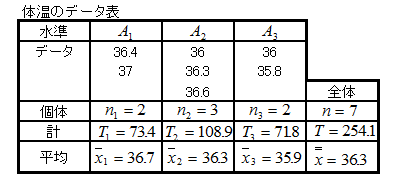
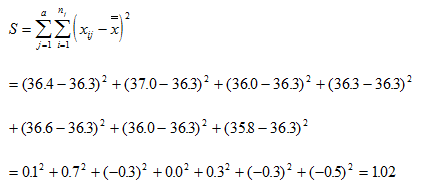
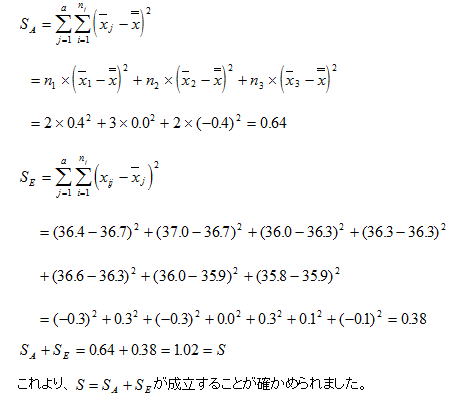

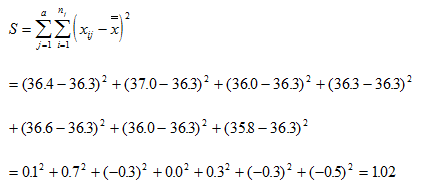
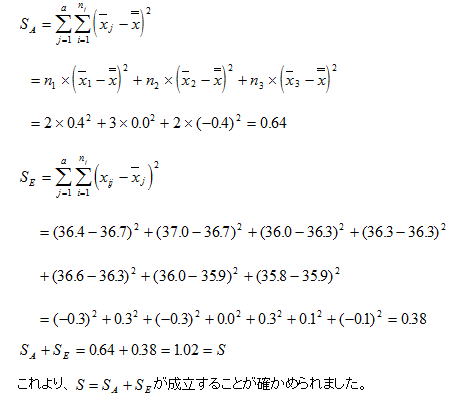
このことから、全体変動が因子間変動と誤差変動に分解できることが分かりました。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。









