母分散と比較値の差の検定
◆母分散と比較値の差の検定◆
母分散と比較値の差の検定の概要
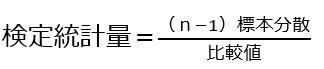
母分散と比較値の差の検定は、1項目(1群)のデータの標本分散と解析者が指定する比較値から、母分散が比較値と異なるかを検証する検定方法である。
母分散の検定は母集団におけるデータが正規分布である場合に適用できる。
母分散の検定は次の手順によって行う。
①帰無仮説を立てる
母分散は比較値と同じ
②対立仮説を立てる
次の3つの内のいずれかにする
・母分散は比較値より大きい
・母分散は比較値より小さい
・母分散は比較値と異なる
③両側検定、片側検定を決める
対立仮説によって自動的に決まる
対立仮説:母分散は比較値より大きい → 片側検定(右側検定)
母分散は比較値より小さい → 片側検定(左側検定)
対立仮説:母分散は比較値と異なる → 両側検定
④検定統計量を算出
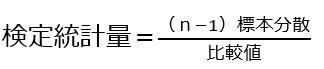
検定統計量は帰無仮説の基に自由度n-1のχ2分布(カイ2乗分布)にしたがう。
⑤p値を算出
⑥有意差判定
p値<有意水準0.05 (5%)
帰無仮説を棄却し対立仮説を採択 → 有意差があるといえる。
有意水準は通常5%を適用するが1%を用いることもある。
有意水準0.05と0.01から有意差判定を次のように行うこともある。
p値<0.01 [**] 有意水準1%で有意差がある
0.01≦p値<0.05 [* ] 有意水準5%で有意差がある
p値≧0.05 [ ] 有意差があるといえない
母分散と比較値の差の検定の結果

【具体例】
ある機械の部品の新製法が開発された。その製法によって作られた部品からランダムに11個を取り出し、重量の標準偏差を計算したところ、42gだった。基準としている重量の標準偏差は30gである。
次の3つの仮説検証について検定せよ。
母集団における部品データは正規分布であるとする。
(1)新製法によって重量のバラツキが30gより大きくなったといえるかを調べよ。
(2)新製法によって重量のバラツキが30gより小さくなったといえるかを調べよ。
(3)新製法によって重量のバラツキは30gと異なるかを調べよ。
【検定結果】
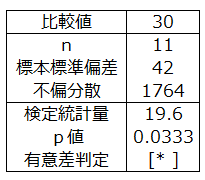
(1)対立仮説:重量のバラツキは30gより大きい → 右側検定を適用

p値 0.0333<有意水準0.05
重量のバラツキは30gより大きいといえる
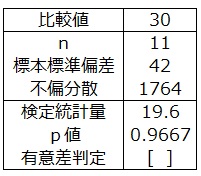
(2)対立仮説:重量のバラツキは30gより小さい → 左側検定を適用

p値 0.9667>有意水準0.05
重量のバラツキは30gより小さいといえない
(3)対立仮説:重量のバラツキは30gと異なる → 両側検定を適用

p値 0.0665>有意水準0.05
重量のバラツキは30gと異なるといえない
母分散と比較値の差の検定の検定統計量はχ2分布になることを検証
ある機械の部品の新製法が開発された。その製法によって作られた部品が10,000個ある。10,000個の部品を母集団とする。母平均は100g、母標準偏差は30g、母分散900g2である。
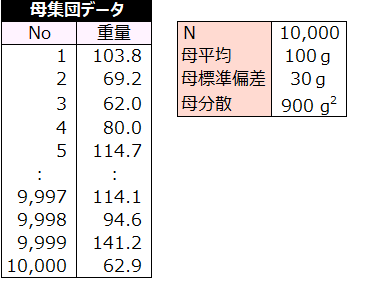
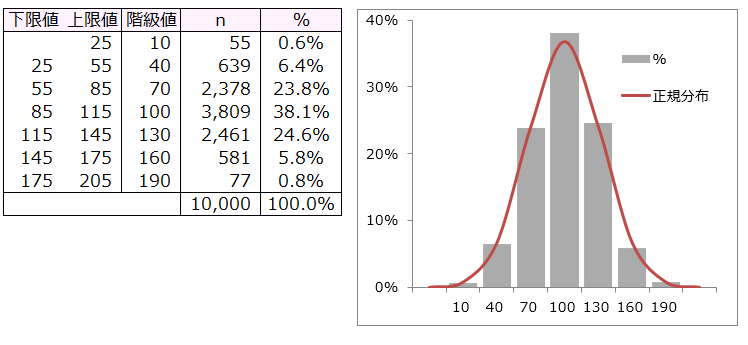
母集団は正規分布である。
検定統計量の算出
母集団(10,000個の部品)から11個をランダムに抽出する調査を実施し、標準偏差、検定統計量を算出した。ただし検定統計量算出式に用いる比較値は母分散900g2とする。この調査を2,000回行い2,000個の検定統計量を求めた。
<計算例> 調査No1の検定統計量
標準偏差で与えられている値を分散に直す
比較値=900 標本分散=612
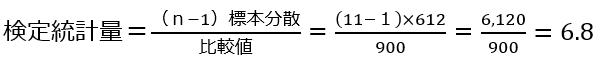
2,000回の標本調査の検定統計量を示す。
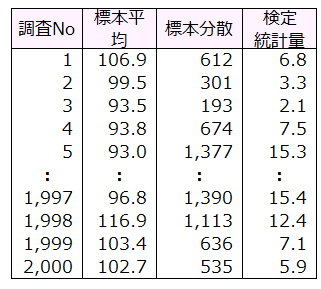
検定統計量の度数分布を作成した。

度数分布のグラフを描いた。
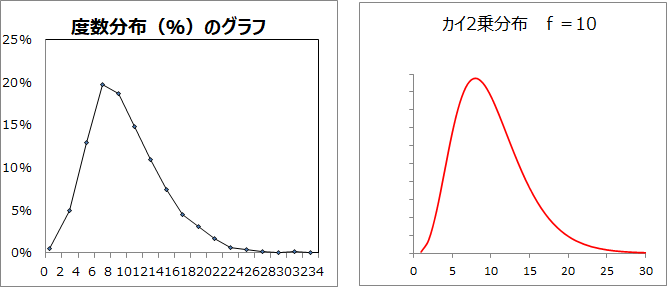
度数分布は自由度n-1=10のカイ2乗分布(χ2分布)になる。
検定統計量は、帰無仮説「部品重量の母分散は900g2である」という仮説のもとにχ2分布になる。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










