ウェルチのt検定
◆ウェルチのt検定◆
ウェルチのt検定の概要
データは数量データとカテゴリーデータに大別されるが、ウェルチのt検定は数量データに適用できる手法である。
ウェルチのt検定は、p値による有意差判定と母平均差分の信頼区間から構成される。
p値による有意差判定とは、2つの母集団から無作為抽出したサンプルの標本平均や標本標準偏差から、その2つ(2群)の母平均が等しいと言えるかをp値によって調べる方法である。
母平均差分の信頼区間とは、標本平均の差分が母集団の差分であると言い切るのは危険であるので標本平均の差分に幅をもたせて推定する方法である。
ウェルチのt検定は、20世紀のイギリスの統計学者 Bernard Lewis Welch がスチューデントのt検定を改良したものである。
ウェルチのt検定は下記条件の基に帰無仮説が正しいと仮定した場合に、サンプルの標本平均や標本標準偏差から計算された検定統計量がt分布に従うことを利用する統計学的検定法である。

母集団の正規性については、t検定同等この検定も頑健だといわれている。それは、サンプルサイズが十分大きければ母集団が正規分布でなくとも検定統計量はt分布に近づくからである。「サンプルサイズが十分大きい」の目安は30で、2群合わせると60である。言い換えれば2群合わせたサンプルサイズが60以上であれば母集団が正規分布でなくてもウェルチのt検定は適用できるということである。
サンプルサイズが60に満たない場合の母平均の差の検定はノンパラ検定を適用する。
5件法(5段階評価)のデータはt検定を適用してよいが、4件法はノンパラ検定を適用するのがよいと思われる。
p値による有意差判定の手順
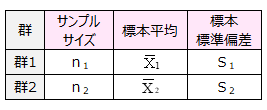
①帰無仮説を立てる
群1の母平均値と群2の母平均値は同じ
②対立仮説を立てる
次の3つの内のいずれかにする
(1)群1の母平均は群2の母平均より大きい
(2)群1の母平均は群2の母平均より小さい
(3)群1の母平均と群2の母平均は異なる
③ 両側検定、片側検定を決める
対立仮説によって自動的に決まる
対立仮説(1) → 片側検定(右側検定)
対立仮説(2) → 片側検定(左側検定)
対立仮説(3) → 両側検定
④ 検定統計量を算出

⑤p値の算出
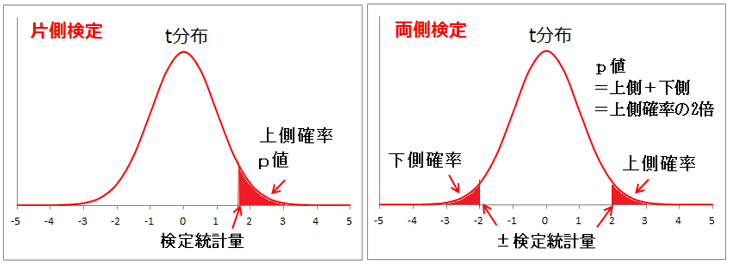
検定統計量は帰無仮説が正しいと仮定した場合にt分布に従う。
t分布において、横軸の値が検定統計量であるときの上側の面積をp値という。
片側検定におけるp値はt分布における検定統計量の上側確率である。
両側検定におけるp値はt分布における検定統計量の上側確率の2倍。
⑥p値による有意差判定
片側検定(右側検定、左側検定)、両側検定いずれも
p値<有意水準0.05
帰無仮説を棄却し対立仮説を採択 有意差があるといえる。
p値≧有意水準0.05
対立仮説を採択できず、有意差があるといえない。
※ 有意水準は0.05が一般的であるが、0.01を適用することもある。
※ 有意差判定を次で示すこともある。
p値<0.01 [**] 有意水準1%で有差がある
0.01≦p値<0.05 [* ] 有意水準5%で有意差がある
p値≧0.05 [ ] 有意差があるがあるとはいえない
母平均差分の信頼区間の手順
信頼区間を次式よって算出する。
(X1-X2)±棄却限界値×標準誤差
標準誤差は「p値による有意差判定の手順」④で示した式である。
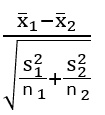
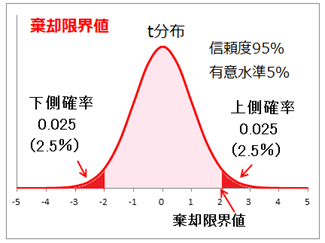
棄却限界値は信頼度95%(有意水準5%)における定数である。
t分布において、上側と下側を合わせた確率が0.05(5%)と
なる横軸の値が棄却限界値である。
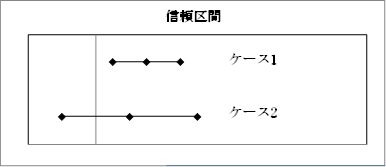
信頼区間を適用しての有意差検定を行う
<ケース1>
信頼区間が0をまたがらない
比較する2群の母平均値は異なる。
<ケース2>
区間が0をまたがる
信頼比較する2群の母平均値は異なるといえない。
ウェルチのt検定の結果
【具体例】
ある県について、小学生6年と中学生1年のお年玉金額の平均に違いがあるかを明らかにしたい。
下記はこの県のお年玉金額を調べた調査結果である。
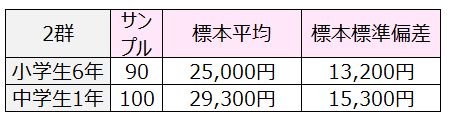
この県全体(母集団)における小学生6年と中学性1年のお年玉金額の標準偏差は異なることが分かっている。
<1> 次の3つについて有意水準5%で調べよ。
(1)お年玉金額の平均は、小学生6年の方が中学1年生より高い。
(2)お年玉金額の平均は、小学生6年の方が中学1年生より低い。
(3)お年玉金額の平均は、小学生6年と中学生1年は異なる。
<2> この県全体の小学生6年と中学生1年のお年玉金額の平均差分の信頼区間を信頼度95%で算出せよ。
小学生6年と中学生1年の比較なので対応のないデータである。
サンプルサイズはn1+n2=190で60より大きい。
母集団における小学生6年と中学生1年のお年玉金額の標準偏差は異なる。
具体例はウェルチのt検定で行う。
【検定結果】
<1> p値による有意差判定
(1)右側検定
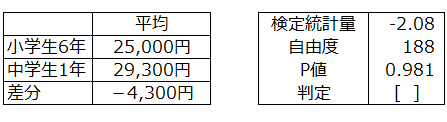
p値>0.05より、
お年玉金額の平均は小学生6年の方が中学生1年より高いがいえない。
(2)左側検定
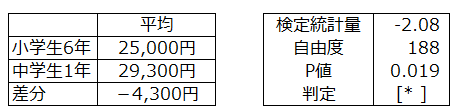
p値<0.05より、
お年玉金額の平均は小学生6年の方が中学生1年より低いがいえる。
(3)両側検定
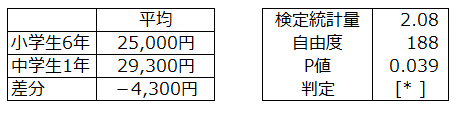
p値<0.05より、
お年玉金額の平均は小学生6年と中学生1年は異なるがいえる。

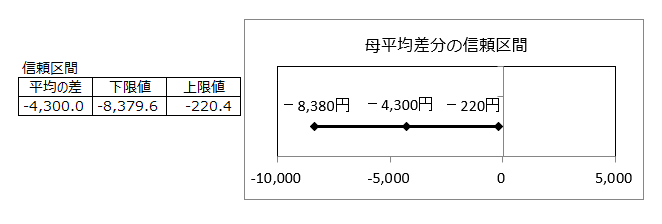
<2> 母平均差分の信頼区間
この地域全体の小学生6年と中学生1年のお年玉金額の平均差分の信頼区間は、信頼度95%で、-8,380円~-220円の間にあるといえる。
信頼区間は0をまたがらないので、お年玉金額の平均は小学生6年と中学生1年は違いがあるといえる。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。











