統計的検定の手順
◆統計的検定の手順◆
統計的検定の仕方を示す。
(1) 母集団に関して主張したい仮説とは逆の仮説 (帰無仮説) を立てる。
(2) その仮説が正しいとしたとき、標本調査の平均や割合より算出される検定統計量の分布を考える。
(3) 調査結果からその検定統計量の値を計算する。
(4) 検定統計量の出現する確率p値を算出する。
(5) p値があらかじめ定めておいた有意水準 (通常5%) より小さければ、帰無仮説を棄却し,
大きければ帰無仮説の判定を保留する。
統計的検定の考え方の具体例で、検定方法の手順について解説する。
<仮説>
仮説をたてる。
主張したいこと(対立仮説)を決める。
対立仮説:「A商品の認知率は60%でない」
逆の仮説である帰無仮説は必然的に決まる。
帰無仮説:「A商品の認知率は60%である」
主張したいことから両側検定か片側検定かを決める。
このテーマの主張したいことは「A商品の認知率は60%でない」なので、両側検定である。
<検定統計量>
母比率の検定の検定統計量を算出する。
母比率の検定の検定統計量は標本割合の基準値である。

<検定統計量の分布>
検定統計量の分布を調べる。
母比率の検定における検定統計量=標本割合の基準値の分布は帰無仮説の基にz分布になる。
※検定する母数が平均、割合、分散などによって検定統計量の分布はz分布、t分布、カイ二乗分布、F分布など異なる。
<p値>
z分布における検定統計量の上側確率から求められる値である。
両側検定と片側検定で異なる。
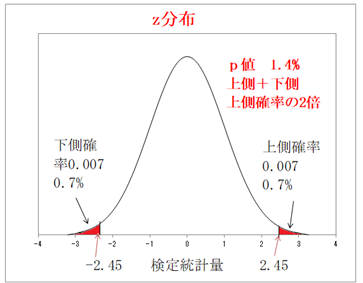
・両側検定の場合のp値 0.014 1.4%
z分布における検定統計量2.45の上側確率の2倍
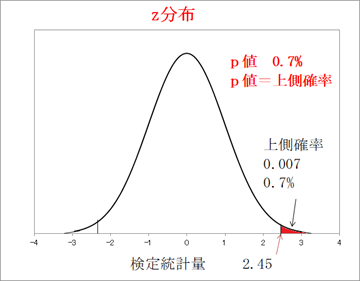
・片側検定の場合のp値 0.007 0.7%
z分布における検定統計量の上側確率
<有意差判定>
p値<有意水準 帰無仮説を棄却し主張したいこと(対立仮説)を採択
有意差があるといえる。
p値≧有意水準 帰無仮説を棄却できず主張したいこと(対立仮説)を採択できない
主張したいことの判定を保留する。
有意差があるかわからい。
「有意差があるといえない」という言い方をしてもよい。
有意水準は通常5%を適用するが1%を用いることもある。
有意水準0.05と0.01から有意差判定を次のように行うこともある。
p値<0.01 [**] 有意水準1%で有意差がある
0.01≦p値<0.05 [* ] 有意水準5%で有意差がある
p値≧0.05 [ ] 有意水準があるといえない
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










