パーセンタイル・四分位偏差

◆パーセンタイル・四分位偏差◆

データを昇順で並べ替えます。小さいほうから数えて任意の％に位置する値をパーセンタイルといいます。（パーセンタイルはパーセント点ともいう。）

また、全体の25％、50％、75％に位置する値を、それぞれ第1四分位点（下ヒンジともいう））、中央値、第3四分位点（上ヒンジともいう）といいます。

第3四分位点から第1四分位点を引いた値を四分位範囲といいます。

四分位範囲を2で割った値を四分位偏差といいます。

四分位範囲、四分位偏差は標準偏差と同様、データのばらつき具合を示します。

下記に示すデータでパーセンタイルの求め方を説明します。

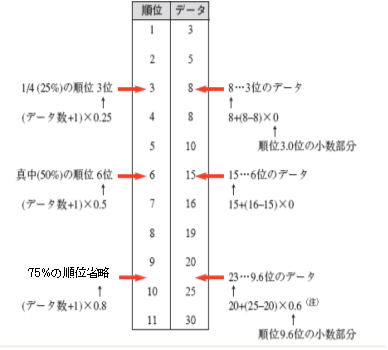
まず始めに、任意の％（50％と80％）に位置するデータの順位について示します。

10個のデータの真ん中（50％→0.5）に位置するデータの順位は　

（10＋1）×0.5＝5.5　で求められます。

4/5（80%→0.8）に位置するデータの順位は

（10＋1）×0.8＝8.8　となります。

一般的にデータ数がｎ個でｐ％に位置するデータの順位は

（ｎ＋1）×ｐ/100　で求められます。

求められた順位の整数部をｑ、小数部をｒとします。

上記例のｑ、ｒはつぎとなります。

次のデータは、ある高等学校１年生11人の懸垂回数を示したものです。

このデータについて、第１四分位点、中央値、第３四分位点、80％におけるパーセンタイル、四分位偏差を求めなさい。

データを並び替える

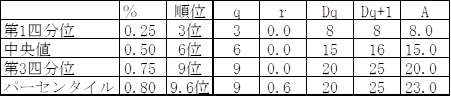
答え）第1四分位点・・・・・・・・・・8回

　　　中央値・・・・・・・・・・・・・15回

　　　第3四分位点・・・・・・・・・・20回

　　　80％におけるパーセンタイル・・23回

　　　四分位偏差・・・・・・・・・・・6回

予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。

マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。

統計学、解析手法の役割から種類、概要までを学びます。

調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。