ウイルコクソンの符号順位和検定

◆ウイルコクソンの符号順位和検定◆

ウイルコクソンの符号順位和検定の概要

ウイルコクソンの符号順位和検定はノンパラメトリック検定のひとつである。この検定をサインランク検定ということがある。

名前が似ているウイルコクソンの順位和検定とは異なる検定法なので注意が必要である。どちらもデータが順序尺度の場合、及び、距離尺度の場合はサンプル数が少ないときに用いられる。

この検定手法は得られた2つのデータ間に対応があるときに用いる検定法である。すなわち、ウイルコクソンの順位和検定はパラメトリック検定でいうところの対応のないt検定、ウイルコクソンの符号順位検定は対応のあるt検定に相当するものである。

この検定は対応する個々のデータの差分の大小を順位に置き換えて統計的検定を行うので、2群の平均値の差というより順位平均値（中央値）の有意差を調べる検定手法といってよいだろう。

ウイルコクソンの順位和検定の検定は次の手順によって行う。

①帰無仮説を立てる

　群1と群2の二つの群の母集団の順位平均値は同じ

②対立仮説を立てる

　次の3つの内のいずれかにする

（1）群1の母集団順位平均値は群2の母集団順位平均値より大きい　

（2）群1の母集団順位平均値は群2の母集団順位平均値より小さい

（3）群1と群2の２群の母集団順位平均値は異なる　

③両側検定、片側検定を決める

対立仮説によって自動的に決まる

対立仮説（1）→ 片側(右側)検定

対立仮説（2）→ 片側(左側)検定

対立仮説（3）→　両側検定

④検定統計量Ｕを算出

⑤ｐ値を算出

サンプルサイズが25以下 サインランク検定表適用

サンプルサイズが26以上ｚ分布適用

⑥有意差判定

ｐ値＜有意水準0.05　2群の順位平均値に差があるといえる

ｐ値≧有意水準0.05 2群の順位平均値に差があるといえない

サンプルサイズが25以下の検定の結果

【具体例】

対象者10人に、脂肪分の量の異なる２種類のアイスクリーム新製品Ａと既存製品Ｂを試食してもらい、10点満点でおいしさを評価してもらった。

新製品Ａのアイスクリームは既存製品Ｂより評価が高いといえるか。

有意水準0.05で検定せよ。

【基本統計量】

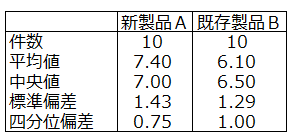
【検定結果】

対立仮説は「ＡはＢより評価は高いか」より、片側検定を行う。

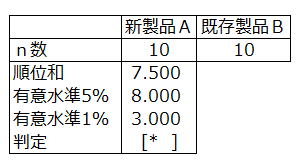
ｎ’＝9は、具体例のｎ数10から評価が同じ回答者数1を引いた値である。

順位和7.5＜8.000より、「ＡはＢより評価は高い」がいえる。

有意水準1％で検定した場合、順位和7.5＞3.000より

「ＡはＢより評価は高い」がいえない。

判定マーク　[**] 有意水準1％で有意差があるといえる。

　　　　　　[* ] 有意水準5％で有意差があるといえる

　　　　　　[　] 有意差があるといえない。

サンプルサイズが26以上の検定の結果

【具体例】

対象者29人に、脂肪分の量の異なる２種類のアイスクリーム新製品Ａと既存製品Ｂを試食してもらい、10点満点でおいしさを評価してもらった。

新製品Ａのアイスクリームは既存製品Ｂより評価が高いといえるか。

有意水準0.05で検定せよ。

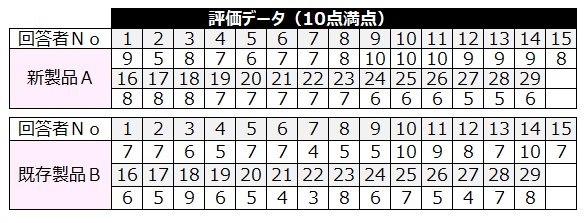
【基本統計量】

【検定結果】

対立仮説は「ＡはＢより評価は高いか」より、片側検定を行う。

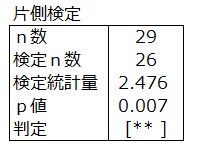
検定ｎ数26は、具体例のｎ数29から評価が同じ回答者数3を引いた値である。

ｐ値0.007＜有意水準0.01より、「ＡはＢより評価は高い」がいえる。

判定マーク　[**] 有意水準1％で有意差があるといえる。

　　　　　　[* ] 有意水準5％で有意差があるといえる。

　　　　　　[　] 有意差があるといえない。

ノンパラメトリック検定の解説一覧に戻る

ウイルコクソンの符号順位和検定