コルモゴロフ・スミルノフの検定

◆コルモゴロフ・スミルノフ検定◆

コルモゴロフ・スミルノフ検定の概要

コルモゴロフ・スミルノフ検定には1標本と2標本の2種類あるがここでは2標本コルモゴロフ・スミルノフ検定を解説する。

2標本コルモゴロフ・スミルノフ検定は、質的データの場合は選択肢が同じ、量的データの場合は階級幅が同じである二つの項目の度数分布について、確率分布の相違を検定する方法である。

階級幅（量的データ）が同じ二つの項目の比較には、母平均の比較と確率分布の比較がある。

この検定は確率分布の比較であって、母平均の比較でない。検定結果がｐ値＜0.05だからと言って２項目の母平均に有意差があるといってはいけない。

適合度の検定は次の手順によって行う。

①帰無仮説を立てる

　二つの項目の度数分布について確率分布は同じ

②対立仮説を立てる

　二つの項目の度数分布について確率分布は異なる

③両側検定のみで片側検定はない

④検定統計量を算出

⑤２標本に累積相対度数を作成し、各カテゴリーについて差を求め、その最大値をDとする。

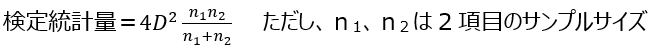
⑥ｐ値を算出

　ｎ₁≧40、ｎ₂≧40の時、検定統計量はカイ2乗分布に従う。

　p値は、カイ二乗分布において検定統計量の上側確率の2倍である。

　ｐ値<有意水準0.05　対立仮説が言える

　ｐ値≧有意水準0.05 対立仮説が言えない

　ｎ₁<40、ｎ₂<40の場合、コルモゴロフ・スミルノフの検定表より、ｎ、有意水準0.05に対応する値を求める。

　求められた値と検定統計量の比較で有意差判定する。

コルモゴロフ・スミルノフ検定の結果

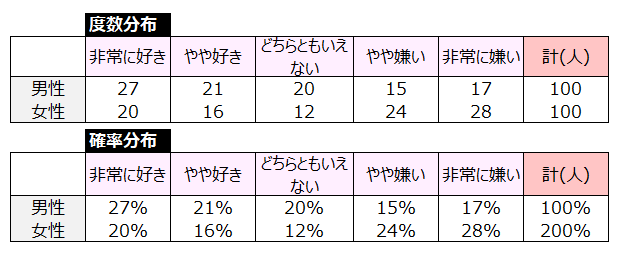
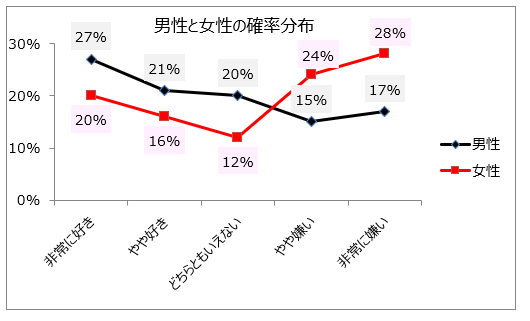
【具体例】

Ａ商品をどの程度好きかを5段階評価で聞いた。

男性100人のＡ商品志向度、女性100人のＡ商品志向度を集計し、度数分布と確率分布を求めた。

Ａ商品志向度の確率分布は男性と女性で異なるかを調べよ。

【検定結果】

ｐ値＜0.05より、Ａ商品志向度の確率分布は男性と女性で異なるといえる。

度数に関する検定の解説一覧に戻る

度数に関する検定でお悩みの方ご相談ください

▼データ分析代行・コンサルティングを承ります

▼ご相談（無料）・お見積はこちらをクリック

予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。

マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。

統計学、解析手法の役割から種類、概要までを学びます。

調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。