統計的検定

◆クラメール連関係数の無相関検定◆

クラメール連関係数の無相関検定の概要

クラメール連関係数は、カテゴリーデータである2項目間のクロス集計表において、2項目間の相関関係を数値で記述する方法である。

クラメール連関相関係数は0から1の間の値で、絶対値が大きいほど相関関係は高い。

クラメール連関係数の無相関検定は母集団のクラメール連関係数が0であるかを検証する検定方法である。

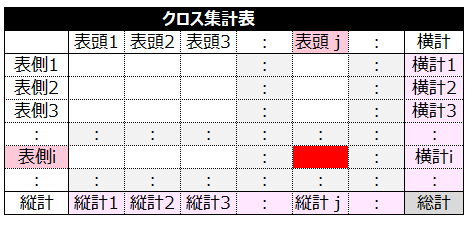
表側ｉ番目、表頭ｊ番目の実測度数をＤijとする。

表側ｉ番目、表頭ｊ番目の期待度数をＥijとする。

Ｅij＝横計i×縦計j÷総計

検定統計量＝Σ（実績度数－期待度数）2／期待度数

自由度ｆ＝（表側カテゴリー数－1）×（表頭カテゴリー数－1）

ただし、ｎはサンプルサイズ

ｋは2項目のカテゴリー数の小さい方の値

検定統計量は自由度ｆのカイ二乗分布（χ²分布）にしたがう。

p値は、χ²分布における検定統計量の上側確率である。

クラメール連関係数の無相関検定の結果

【具体例】

所得階層と支持政党とのクロス集計の結果を示す。

所得階層と支持政党のクラメール連関係数を求めよ。

母集団におけるクラメール連関係数は0でない相関関係があるかを明らかにせよ。

【検定結果】

帰無仮説：所得階層と支持政党のクラメール連関係数は0である。

対立仮説：所得階層と支持政党のクラメール連関係数は0でない。

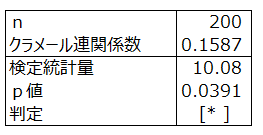
クラメール連関係数は0.1587である。

ｐ値0.0391＜0.05より

帰無仮説を棄却し対立仮説を採択する。

所得階層と支持政党の母集団におけるクラメール連関係数は0でない相関があるといえる。

相関に関する検定の解説一覧に戻る

統計的有意差検定でお困りの方ご相談ください

▼データ分析代行・コンサルティングを承ります

▼ご相談（無料）・お見積はこちらをクリック

予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。

マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。

統計学、解析手法の役割から種類、概要までを学びます。

調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。