コクランのQ検定
◆コクランのQ検定◆
コクランのQ検定の概要
コクランのQ検定は、対応のある3つ以上の2値変数(カテゴリーデータ)について、すべての変数間で割合に差があるかどうかを調べる方法である。検定手法としては、マクネマー検定を拡張したものなので、2変数に対しても用いることができるが、その場合はマクネマー検定に一致する。
検定の手順
①帰無仮説を立てる
母集団における各変数の割合は全て等しい
②対立仮説を立てる
母集団における各変数の割合は、全て等しいというわけではない。
※両側検定、片側検定の概念がない。
③検定統計量を算出
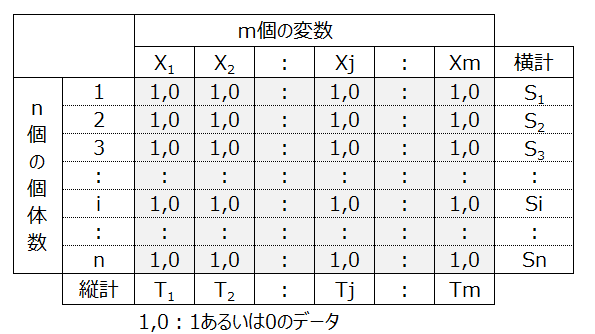
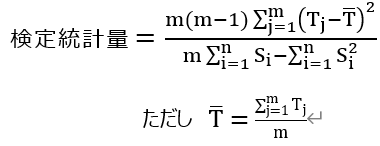
④p値の算出
検定統計量は帰無仮説が正しいと仮定した場合に自由度m-1のカイ2乗分布に従う。
カイ2乗分布において、横軸の値が検定統計量であるときの上側の面積をp値という。
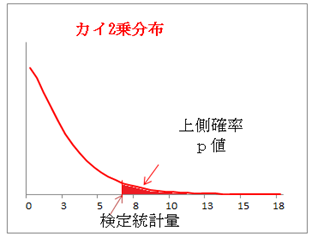
⑤p値による有意差判定
p値<有意水準0.05
帰無仮説を棄却し対立仮説を採択 有意差があるといえる。
p値≧有意水準0.05
対立仮説を採択できず、有意差があるといえない。
※ 有意水準は0.05が一般的であるが、0.01を適用することもある。
※ 有意差判定を次で示すこともある。
p値<0.01 [**] 有意水準1%で有差がある
0.01≦p値<0.05 [* ] 有意水準5%で有意差がある
p値≧0.05 [ ] 有意差があるといえない
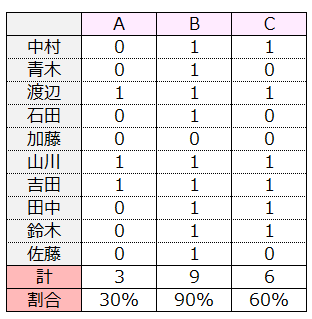
コクランのQ検定の結果
【具体例】
10人の来場者に、3つの商品A,B,Cについて好き(1)、嫌い(0)を聞いた。
3つの商品の好まれ方に差があるかを検定せよ。

p値<0.05より、
3つの商品の好まれ方に差があるといえる。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。









