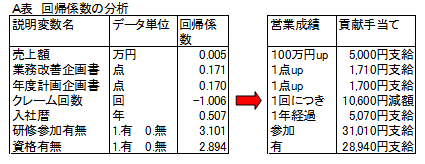
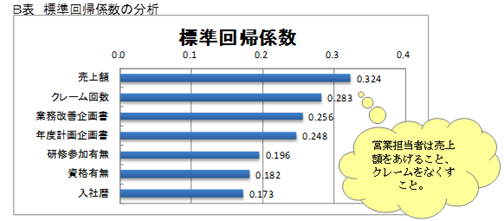
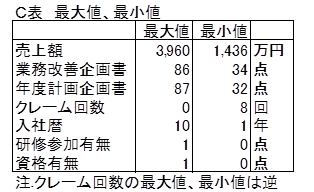
《重回帰分析(3/3) 》
係数矛盾現象が起こる例題
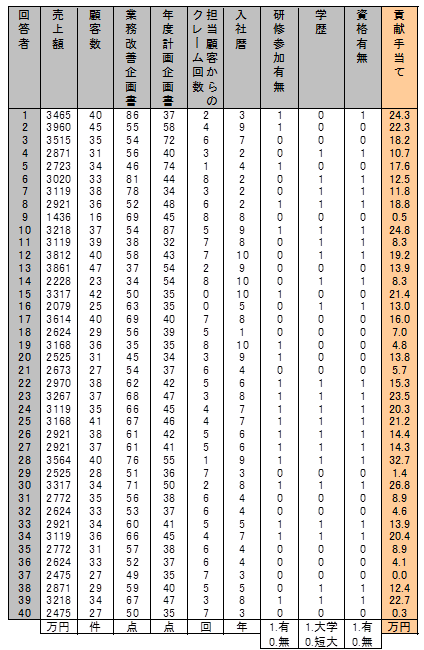
係数矛盾現象
説明変数の選択方法
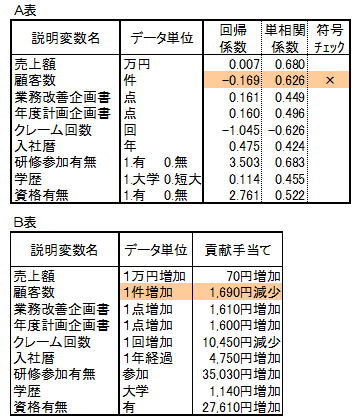
①説明変数相互で相関の高い変数を探し、どちらかの変数を落とします。
具体的には相関が0.7以上のときは、どちらかを落とします。この値も1つの目安です。落とし方は、落とす候補になった変数と目的変数との相関をそれぞれ調べて、相関の低い方を落とします。
下記の例では、X1とX2との相関が高いので、どちらかを落とすことになります。 YとX1、YとX2の相関を比べるとYとX2の方が低いので、X2を落とします。

②データが全て同じ値の説明変数は落とします。
アンケート調査で段階評価(1.良い 2.どちらともいえない 3.悪い)を説明変数とした場合などに、全員が「2.どちらともいえない」に回答する、といったことがまれにあります。この場合、この変数のデータはすべて「2」となり、この変数は重回帰分析に使えません。データがすべて同じだと標準偏差が0になるので、重回帰分析を行う前に標準偏差を計算してチェックし、標準偏差0の変数は落としてください。
①将来設定ができない説明変数を落とします。
具体例を紹介します。
いま、ある売上予測を行うために、広告費、営業担当者数、他社競合商品の売上額を説明変数にとり、重回帰分析を行ったところ、決定係数が0.9となる重回帰式を求めることができました。さっそくこの式を用いて来年度の売上予測を行うことにしました。ところが、広告費、営業担当者数については来年度の設定ができたものの、競合商品の売上額は来年度どうなるかわからず、先へ進むことができませんでした。
このような結果を避けるために、重回帰分析を予測に使う場合、将来設定ができない説明変数は用いないことが一般的です。ただし、"競合商品の売上額がいくらまで上がると、我社の売上額がこれだけ下がる"といったシミュレーション分析を行う場合は、将来設定ができない説明変数を意図的に用いることもあります。
②施策上不必要とした説明変数を落とします。
貢献手当ての学歴は給与の基本給には反映されても営業成績に反映されるものでないと判断し、学歴は落としました。
係数矛盾現象の起こらない重回帰式
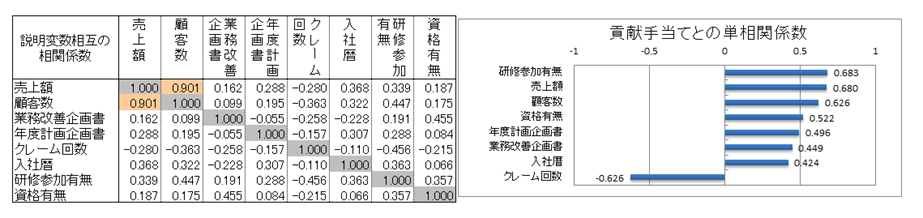
説明変数と貢献手当ての相関は、絶対値で0.3を上回っているので、全て選択します。
説明変数相互の相関の絶対値で0.7以上は、売上額と顧客数です。売上額と貢献手当ての相関は0.680、顧客数と貢献手当ての相関は0.626なので、相関の低い顧客数を落とします。
絞り込んだ説明変数で重回帰式を求め、回帰係数と単相関係数との符号チェックをしました。
係数矛盾現象が起こらない重回帰式となりました
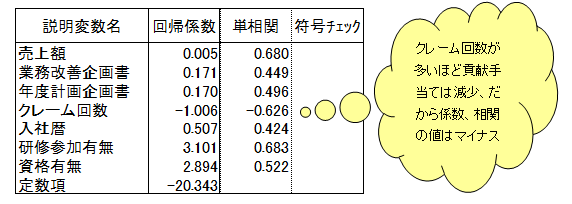
重回帰式の検討