《重回帰分析(2/3) 》
説明変数の目的変数に対する貢献度
回帰係数は、実績値と理論値ができるだけ近くする値であることがわかりました。ところが、この係数の役割はそれだけでなく、それぞれの説明変数の目的変数に及ぼす貢献度も導いてくれます。
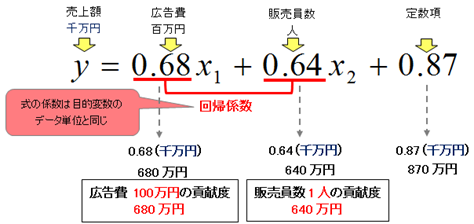
回帰係数にはデータ単位があり、目的変数のデータ単位と同じになることを知っておいてください。
広告費の係数 0.68(千万円) → 680万円
販売員数の係数 0.64(千万円) → 640万円
広告費のデータ単位は「百万円」、販売員数のデータ単位は「1人」でした。つまり、回帰係数から、広告費を百万使うと売上額が680万円、販売員数を1人投入すると640万円増えることがわかります。このように、回帰係数から『説明変数の目的変数に対する貢献度』がわかります。
回帰係数の値の大小を比較してはいけない
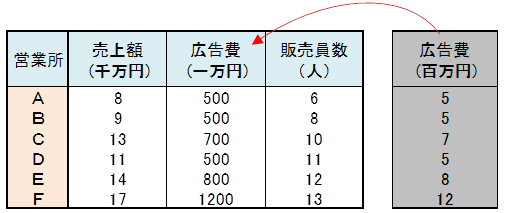
先ほどの売上額と販売員数のデータ単位はそのままで広告費のデータを一万円にして重回帰分析を行い、広告費が百万円の場合の重回帰分析の結果と比較してみました。
販売員数の係数、定数項は一致、データ単位を換えた広告費の係数が不一致となりました。不一致の理由を調べてみましょう。
広告費のデータ単位が百万円のときに見込まれる売上額は680万円ですので、データ単位が1/100の一万円になれば、見込める売上額も1/100の6.8万円となります。これより係数も1/100の0.0068となりました。
データ単位が変われば係数の値も変わることを理解してください。
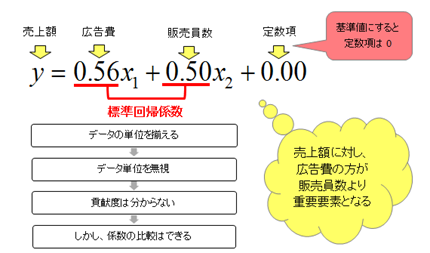
したがって、関係式の回帰係数を比較し、値が大きい説明変数ほど目的変数に貢献しているとか重要であるいうことはいえません。
重回帰分析では、回帰係数とは別の統計量「標準回帰係数」を算出し、この値を使って売上を予測するのに重要な説明変数のランキング(順番)を把握します。

説明変数の重要度ランキング/標準回帰係数
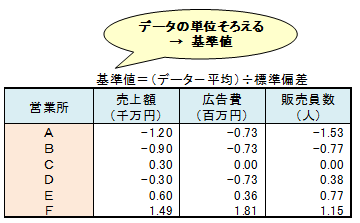
前のデータ(広告費のデータ単位が一万円の方)を基準値にして重回帰分析を行います。求められた係数を標準回帰係数といいます。
前の「広告費が一万円」の場合の係数、広告費0.0068と販売員数0.64とを比較し、広告費の係数の方が小さいから重要でないということはいえません。標準回帰係数では、広告費0.56と販売員数0.50とを比較し、広告費の係数の方が大きいので重要であるということがいえます。
注.基準値データで重回帰を行うと定数項は必ず0になります。
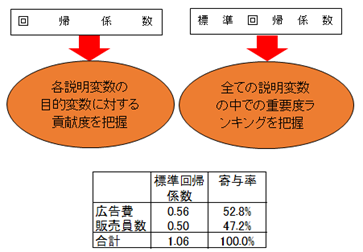
標準回帰係数の絶対値の合計を算出します。各標準回帰係数の合計に占める割合を算出します。この値を寄与率といいます。寄与率は、各説明変数の目的変数に対する重要度を示すものです。
重回帰分析の精度/決定係数
重回帰分析は、実績値と理論値とが近くなるように関係式の係数を見つける手法であることを、先に述べました。
それでは、重回帰分析を適用すれば、どんな場合でも実績値と理論値が近くなるでしょうか。結論からいうと、用いる説明変数が目的変数に関係のないものばかりであれば、理論値を実績値に近づけることはできません。
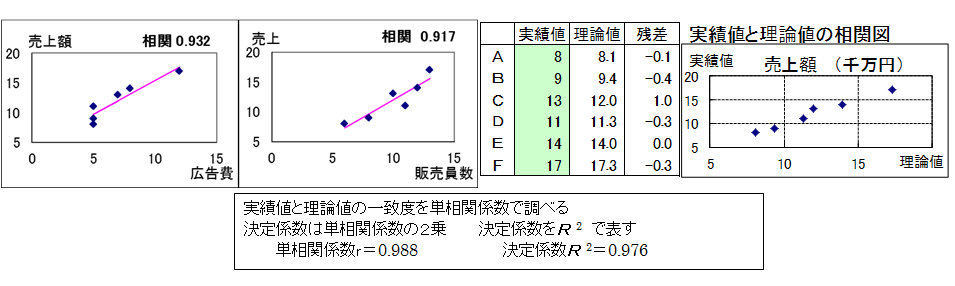
売上額のデータを次に示す相関図で表してみると、広告費が大きければ売上額が大きくなり、両者に高い相関があることがわかります。同様に販売員数と売上額の相関図から、両者の間にも高い相関があることがわかります。このように、売上額と相関の高い説明変数を用いたので、実績値と理論値とは近づいたのです。
仮に、売上額と相関のない店長のゴルフのハンディや年齢を説明変数にしたら、実績値と理論値とは近づきません。
上手な説明変数の選択方法は後ほど説明することにして、ここでは、説明変数の選択が良ければ実績値と理論値が近づき、重回帰分析を首尾よく終了できることを理解してください。
実績値と理論値が近くなるほど、「分析の精度」が良い、あるいは重回帰式の当てはまり具合が良いともいいます。
予測は重回帰式を使って行うので、精度の悪い重回帰式ではそれができないということになります。
分析の精度を一つの数値で表すことができれば、この尺度を用いて、求められた重回帰式が予測に使えるかどうかを判断することができます。
売上額の分析の精度を調べてみましょう。
重回帰分析で求めた売上額の実績値と理論値を再掲します。両者の相関図を描き、相関係数を求めてみます。この相関係数を重回帰分析の相関ということで、重相関係数といいます。重相関係数の自乗を決定係数といいます。
決定係数を分析の精度に用います。決定係数の値は0から1の間で、値が大きいほど分析精度は良いといえます。
決定係数はいくつ以上あればよいか
決定係数はいくつ以上あれば良いかと、よく質問されます。残念ながらいくつ以上あれば良いという統計学的基準はありません。この基準は、分析者が経験的な判断から決めることになります。
先生は、次のように決めていますが、皆さんはいかがでしょうか。

決定係数が高いとき、モデル(重回帰式)の説明力が高いという、言い方をします。
このとき、決定係数の値を%表示して、説明力は80%(決定係数は0.8の場合)であるという、言い方をする人がいますが、これは間違いです。正しくは、「決定係数は0.8で基準の0.5を大きく上回り、モデルの説明力は非常に高い」です。
予測
決定係数が高ければ(先生は0.5以上)、重回帰式は予測に使えると判断します。
前述の売上額の重回帰式は、
『決定係数は0.976で基準の0.5を大きく上回りましたので、この重回帰式は予測に使える』
と判断しました。
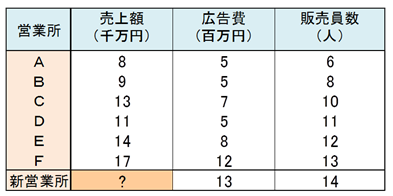
この重回帰式に新営業所の広告費、販売員数を代入し、売上額を予測しました。