重回帰分析
《重回帰分析(1/3) 》
重回帰分析とは
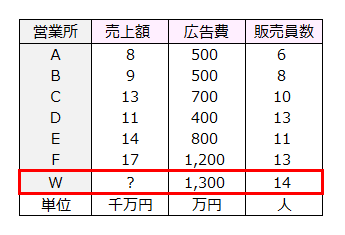
下記表は、ある会社の営業所における売上額と広告費と販売員数を示したものです。
この表のデータを見ると、投入する広告費や販売員数が多い営業所は売上額が大きく、投入量が少ない営業所は売上額が小さくなっていることが推察できます。
この傾向を踏まえて、今度新設するW営業所の広告費を1300万円、販売員数を14人としたとき、この営業所の売上額はどれほどになるかを予測したいと思います。
≪例題1≫
この目的を解決してくれるのが重回帰分析です。
予測したい変数、この例では売上額を目的変数といいます。
目的変数に影響を及ぼす変数、この例では広告費と販売員数を説明変数といいます。
重回帰分析で適用できるデータは、目的変数、説明変数どちらも数量データです。
重回帰分析は、目的変数と説明変数の関係を関係式で表します。
重回帰分析における関係式を重回帰式(モデル式ともいう)といいます。
この例の重回帰式は、次となります。
売上額=0.00786×広告費+0.539×販売員数+1.148
重回帰分析はこの重回帰式を用いて、次の事柄を明らかにする解析手法です。
① 予測値の算出
② 関係式に用いた説明変数の目的変数に対する貢献度
回帰係数の算出の考え方
重回帰式の係数を回帰係数といいます。
まずはじめに回帰係数がどのような考え方で求められているかを説明します。
回帰係数の算出方法を解説する前に、次のクイズにお答え下さい。

いかがでしょうか。答はいくつでもありますね。
たとえばア=0.005、イ=0.3、ウ=3.7 とすれば
8= 0.005 ×500+ 0.3 ×6+ 3.7
が成立します。
続けて次のクイズにお答えください。

クイズ②として、クイズ①と同じく、ア=0.005、イ=0.3、ウ=3.7を代入してみます。
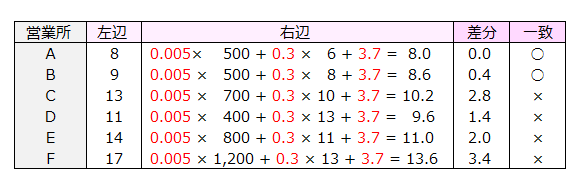
左辺(売上額)から右辺を引いた差分で一致度を見ると、AとBはほぼ一致していますが、他の営業所は差分が1以上で一致していません。
残念ながら、この答えは正解といえません。
ご覧のように、手計算でこのクイズを解くのは大変です。これを解決してくれるのが重回帰分析なのです。
それでは、重回帰分析が導いてくれた重回帰式に広告費と販売員数を代入してみます。
求められた値(左辺)と売上額(右辺)との差分を調べてみましょう。
売上額=0.00786×広告費+0.539×販売員数+1.148
※ 差分:左辺から右辺を引いた絶対値(マイナスはプラスにした値)です。
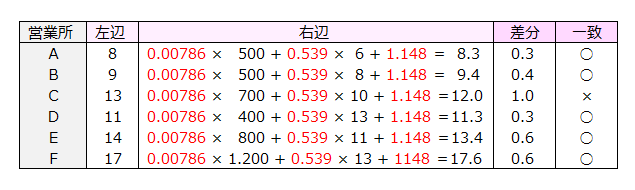
※ 一致:差分が1未満を一致していると考え○、1以上を×としました。
左辺と右辺とはぴったりは一致しませんが、どの営業所についてもほぼ近い値なっています。重回帰分析では、左辺の売上額を実績値、右辺の計算値を理論値といいます。重回帰分析とは、実績値と理論値ができるだけ近くなるように、重回帰式の係数をみつける解析手法です。
理論値、残差で個体を評価する
理論値は投入した広告費や販売員数に見合った売上額で、売上ポテンシャルと考えられます。
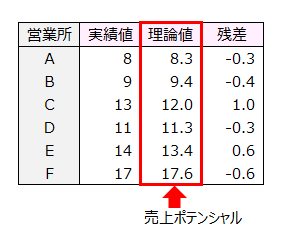
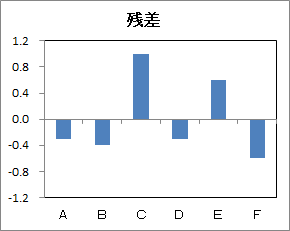
営業所の売上額実績(13千万円)は売上ポテンシャル(12千万円)を上回っています。営業活動から想定できる売上を超えたので「ガンバッタ」の花丸を付けることが出来ます。
逆に、F営業所の売上実績(17千万円)は売上ポテンシャル(17.6千万円)を下回り、営業活動から想定できる売上を超えられなかったので、「ガンバレナカッタ」の黒星を付けることになります。
売上額から理論値を引いた値を残差といいます。
残差のグラフから、営業所別の評価ができます。とりわけ、Cはよく、Fは悪かったといえます。
決定係数により予測精度を調べる
重回帰分析は、実績値と理論値とが近くなるように重回帰式の係数を見つける手法であることを述べました。
それでは、重回帰分析を適用すれば、どんな場合でも実績値と理論値が近くなるのでしょうか。結論からいうと、用いる説明変数が目的変数に関係のないものばかりであれば、理論値を実績値に近づけることはできません。
「例題1」のデータを次に示す相関図で表してみると、広告費が大きければ売上額が大きくなり、両者に高い相関があることがわかります。同様に販売員数と売上額の相関図から、両者の間にも高い相関があることがわかります。
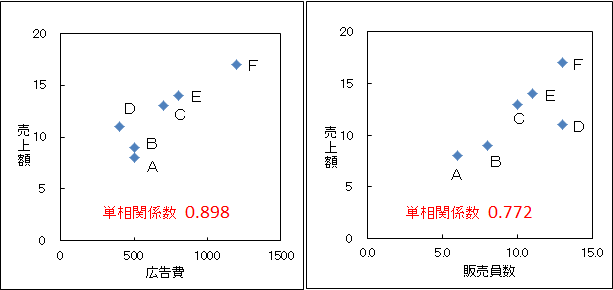
このように、売上額と相関の高い説明変数を用いたので、実績値と理論値とは近づいたのです。
仮に、売上額と相関のない営業所所長のゴルフのハンディや年齢を説明変数にしたら、実績値と理論値とは近づきません。
上手な説明変数の選択方法は後ほど説明することにして、ここでは、説明変数の選択が良ければ実績値と理論値が近づき、重回帰分析を首尾よく終了できることを理解してください。
実績値と理論値が近くなるほど、「分析の精度」が良い、あるいは重回帰式の当てはまり具合が良いともいいます。
予測は重回帰式を使って行うので、精度の悪い重回帰式では予測ができないということになります。
分析の精度を1つの数値で表すことができれば、この尺度を用いて、求められた重回帰式が予測に使えるかどうかを判断することができます。
「例題1」について分析の精度を調べてみましょう。
・残差平方和
「例題1」の残差と残差の2乗を示します。
お答えいたします。
関係式の係数の求め方(1)の回答、0.4、0.5、3を代入してみます。
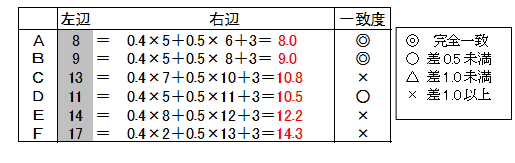
残念ながら、この答だと、6つの営業所中3つはほぼ合いましたが、3つははずれです。このように、手計算でこの問題を解くのは大変です。これを解決してくれるのが重回帰分析なのです。
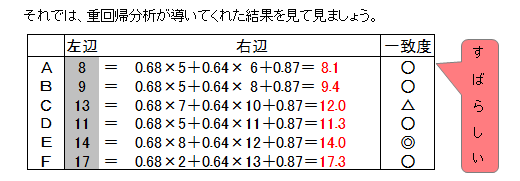
左辺と右辺はぴったりとは一致しませんが、どの営業所についてもほぼ近くなっています。







