《数量化2類(2/3) 》
カテゴリースコアは関係式の係数
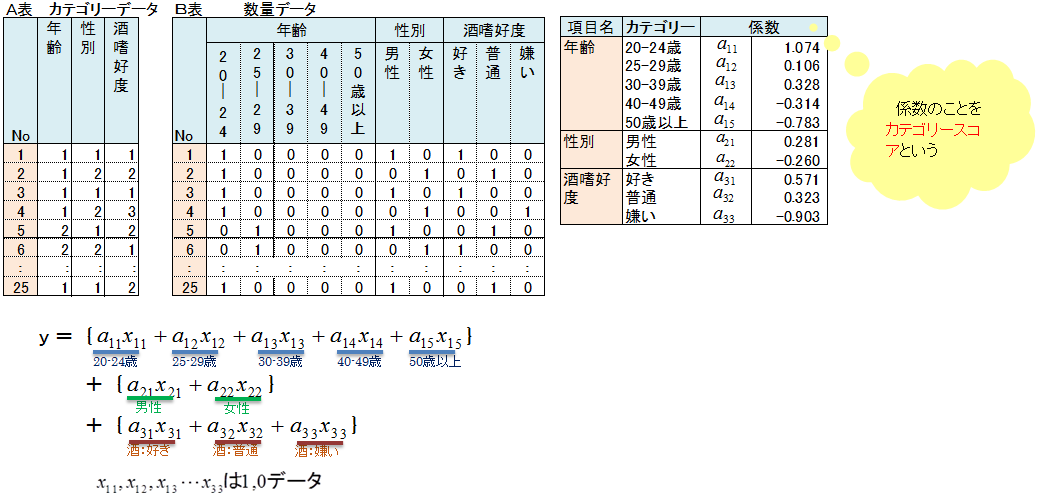
A表はカテゴリーデータです。
B表はカテゴリーデータを1,0の数量データに変換したものです。
関係式はB表のデータに対するものです。関係式の係数はカテゴリースコアです。
サンプルスコア
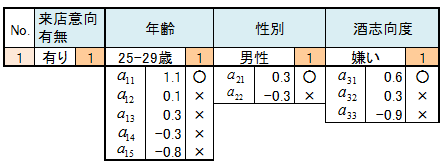
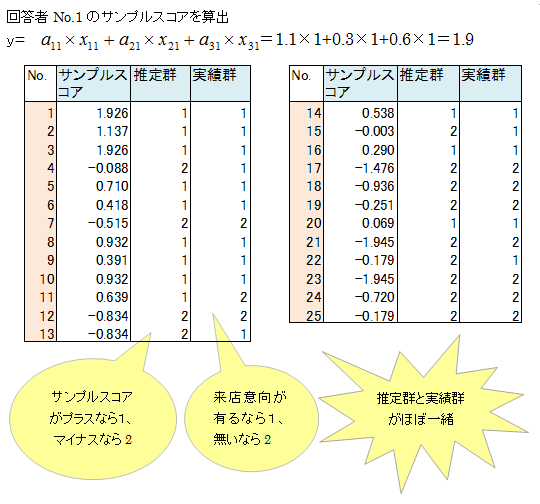
S1の人のデータを関係式に代入してYを求めます。求められたYをサンプルスコアといいます。全ての人についてサンプルスコアを求めます。
サンプルスコアの値が大きい人ほど来店意向度が高い人といえます。値がプラスの人を来店意向層、マイナスの人を来店未意向層と名称します。下記表の推定群で、来店意向層を1、来店未予定層を2として記載しました。
実績群は来店意向の回答データです。推定群と実績群はほぼ一致しています。言いかえれば、カテゴリースコアは推定群と実績ができるだけ一致すように求められたものです。
分析精度
分析精度を調べる方法を二つ示します。
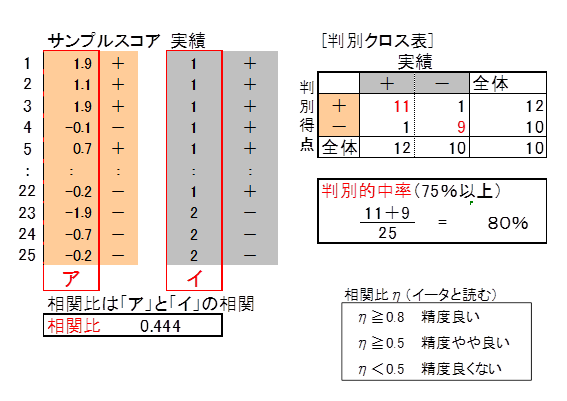
一つは、実績値(来店意向有無)とサンプルスコアとの相関比です。相関比の値が大きいほど分析精度は高く、基準の0.5を上回れば関係式は予測に使えると判断します。
相関比はいくつ以上あれば良いかと、よく質問されます。残念ながらいくつ以上あれば良いという統計学的基準はありません。この基準は、分析者が経験的な判断から決めることになります。先生は、右の表のように決めていますが、皆さんはいかがでしょうか。
もう一つは、判別クロス表を用いる方法です。判別クロス表は、サンプルスコアの符号「+、-」と来店意向有無とをクロス集計したものです。下記の判別クロス集計表の赤表示の数値は実績値とサンプルスコアの符号が一致した人数を示しています。一致人数の全人数に占める割合を判別的中率といいます。判別的中率の値が大きいほど分析精度は高く、基準の75%を上回れば関係式は予測に使えると判断します。
判別的中率、相関比両方が基準の値を上回るのが理想です。しかしこの例題のように片方だけが基準を下回っても関係式を適用する場合、予測の精度がやや劣ることを認識してください。
説明変数の目的変数に対する重要度
来店意向の例題の説明変数の項目数とカテゴリー数を再確認します。項目数は3つ、カテゴリー数は10です。
10個のカテゴリーの目的変数のカテゴリーへの近さ(関連性)は、カテゴリースコアで把握できました。
3個の項目の目的変数に対する重要度ランキングは、数量化1類で学んだレンジ、寄与率で把握できます。
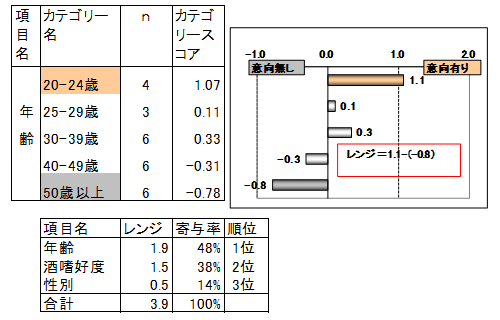
レンジは当該項目のカテゴリースコアの最大値と最小値との差によって求められます。年齢は20-24歳のカテゴリースコアが1.1で最大、50歳以上が-0.8で最小、したがってレンジは1.1-(-0.8)=1.9となります。
各項目のレンジのレンジ合計に占める割合を寄与率といいます。レンジ、寄与率が大きい項目ほど、目的変数への影響度が大きい、重要な項目だといえます。
全ての項目についてレンジ、寄与率を求め、下記に示しました。来店意向有無には年齢が最も影響し、次に酒嗜好度、性別が続きます。
年齢が高くなるほどカテゴリースコアが大きくなる傾向の中で、25-29歳のカテゴリースコアは傾向から外れています。この結果は、25-29歳の意向度が30-39歳の意向度に比べ低い事実なのか、25-29歳のn数が少ないことにより起こる現象かまよいます。
このような悩みを解消するためには、各カテゴリーのn数を多くすることです。
注.数学的な意味合いで確保したいn数は3以上です。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










