《ロジスティック回帰(4/4) 》
標準誤差
説明変数、定数項について標準誤差が出力されます。標準誤差はWald検定の統計量や信頼区間を算出するときに用いられます。
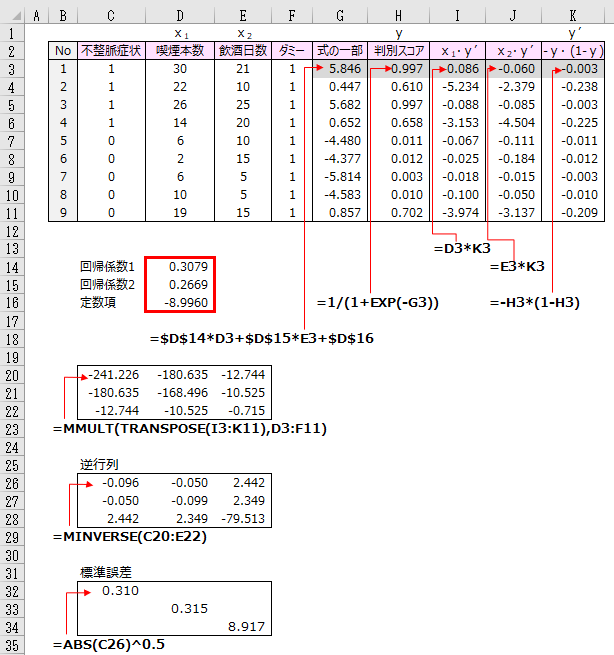
標準誤差の求め方を示します。
ロジスティック回帰の各種統計量の求め方
不健康有無のデータで、各種統計量の計算方法を示します。
[対数尤度の合計]を最大化した値をLLと表現します。
LL=-2.168
-2LLを逸脱度といいます。
-2LL=4.336
モデル選択基準AICは次式によって求められます。
AIC=-2LL+2×(説明変数個数+1)
不健康有無のAIC=-2×(-2.168)+2×(2+1)=4.336+6=10.336
AICの第1項はモデルのあてはまりのよさ、第2項は変数の増加に伴うペナルティーを表し、AICは小さいほど望ましいといえます。
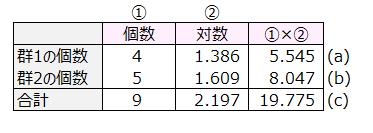
LL0=(a)+(b)-(c)=-6.1827
寄与率=(-2LL0-(-2LL))/(-2LL0)
-2LL0=12.365、 -2LL=4.336
=(12.365-4.336)÷12.365=8.029÷12.365=0.649
寄与率が高いほど判別精度は良いといえます。
検定統計量=-逸脱度-2k
k= 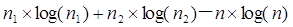
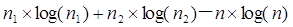
ただし、 は群1、群2、全体の個体数
k=4×log(4)+5×log(5)-9×log(9)
=4×1.386+5×1.609-9×2.197=5.544+8.047-19.775=-6.183
検定統計量=-4.336-2×(-6.183)=-4.336+12.368=8.029
自由度=説明変数個数=2
検定統計量は自由度2のカイ2乗分布に従います。
カイ2乗分布における、検定統計量の上側確率p値を求めます。
Excel関数 =CHIDIST(8.032,2) Enterキー → 0.0181
p値=0.0181<0.05 より モデルは観測データの判別に適合していると判断できます
検定統計量は自由度2のカイ2乗分布に従います。
カイ2乗分布における、検定統計量の上側確率p値を求めます。
Excel関数 =CHIDIST(8.032,2) Enterキー → 0.0181
p値=0.0181<0.05 より モデルは観測データの判別に適合していると判断できます。
目的変数1,0データと判別スコアの残差を算出します。
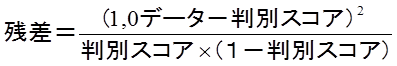
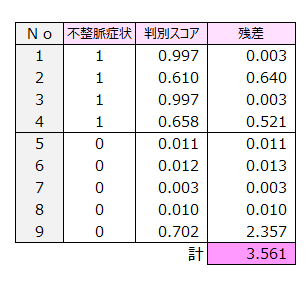

「計」の3.561をピアソン残差といいます。
自由度=n-説明変数個数-1
=9-2-1=6
検定統計量は自由度2のカイ2乗分布に従います。
カイ2乗分布における、検定統計量の上側確率p値を求めます。
Excel関数 =CHIDIST(3.561,6) Enterキー → 0.736
p値=0.0181>0.05 より モデルは観測データの判別に適合していると判断できます。
※ ピアソン残差の検定はp値>0.05で有意なので注意されたい
※ 逸脱度は自由度(n-説明変数の個数-1)のカイ2乗分布に従います。
この検定の判定はp値<0.05で有意です。
回帰係数の有意性を確認するために用いられる検定です。
回帰係数を標準誤差で割ったものを2乗した値をWald–squareといいます。
- 帰無仮説 回帰係数は0である。
- 対立仮設 回帰係数は0でない。
- 検定統計量 Wald–square=(回帰係数÷標準誤差 )2
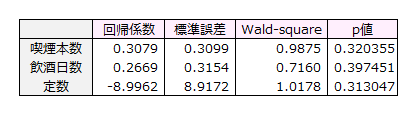
検定統計量は自由度1のカイ二乗分布に従います。
p値 Excelの関数「=CHIDIST(検定統計量,1)」で求められます。
喫煙本数、飲酒日数いずれも、p値>0.05より、帰無仮説を棄却できず、
対立仮設を採択できません。
喫煙本数、飲酒日数の回帰係数はいずれも有意でなく、不整脈有無の判別に寄与しているといえません。
説明変数のデータ単位が全て同じ場合はオッズ比は寄与順位に適用できます。
データ単位が異なる場合、重回帰分析同様、回帰係数の単純比較はできません。
(重回帰の場合は標準回帰係数で寄与順位をします。)
Wald統計量は(回帰係数÷標準誤差)の2乗で検定統計量です。
標準誤算で割ることによって基準化され、寄与順位に適用できます。
回帰係数CI 95% 下限値 b1=回帰係数-1.96×標準誤差
上限値 b2=回帰係数+1.96×標準誤差
オッズ比 95% 下限値= e b1
上限値= eb2
99%CIは定数1.96を2,58として計算します。
不健康有無の喫煙本数のオッズ比95%CIを求めます。
回帰係数CI 95% 下限値 b1=0.3079-1.96×0.3099=-0.2994
上限値 b2=0.3079+1.96×0.3099=0.9152
オッズ比 95% 下限値= e-0.2994=0.7413
上限値= e0.9152 =2.4973
同様の計算で飲酒日数のオッズ比の95%CIを求めます。
オッズ比 95% 下限値=0.7038
上限値=2.4231
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










