《ロジスティック回帰(3/4) 》
ロジスティック回帰の事例
すでに確認されている不整脈症状が「ある患者」のグループと,「ない患者」のグループとにパソコン診断を行います。診断は、喫煙有無、飲酒有無、ギャンブル嗜好についてのアンケートに回答してもらうものです。
下記に20人の診断結果を示しました。
下記データについて不整脈症状有無と診断項目との関係を調べ,不整脈症状であるかどうかを判別するモデル式を作ります。このモデル式をパソコンにセットします。あとは来院した人がパソコンの質問に回答すると,その回答はモデル式にインプットされ,不整脈症状の有無が判定されます。
この事例はモデル式の作り方、モデル式を使っての予測方法を示したものです。
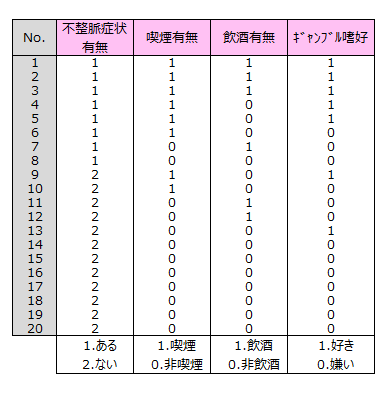
目的変数である不整脈症状有無をカテゴリーデータ、説明変数である喫煙有無、飲酒有無、ギャンブル嗜好を1点、0点の数量データとして、ロジスティック回帰を適用します。
ロジスティック回帰の回帰係数、オッズ比を示します。
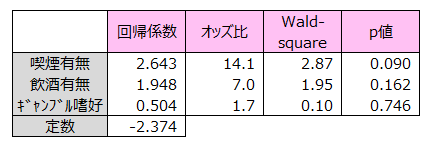
回帰係数はモデル式の係数です。
オッズ比は説明変数の目的変数への影響度を調べる尺度です。値が大きいほど影響度が高い項目といえます。オッズ比から、不整脈症状の原因要因の1位は喫煙の有無で、次に飲酒の有無となります。ギャンブル嗜好は、不整脈症状にそれほど影響がないことがわかります。
Wald-squareは検定統計量です。この値からp値が算出されます。
p値は母集団において説明変数が有意であるかを調べる値です。p値<0.05である項目は、不整脈症状有無の判別に有意であるといえます。
喫煙有無のオッズ比が14.1と大きいにも関わらず、p値>0.05です。これはサンプルサイズが20人と小さく、有意であるかどうか判断できないと解釈します。
ここで、分割表、リスク比、オッズ比を計算してみます。
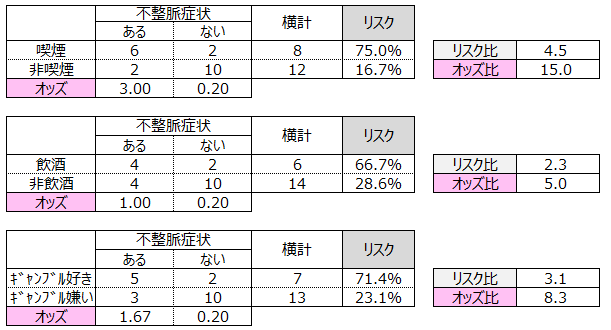
オッズ比を比較します。両者の順位の違いがみられました。
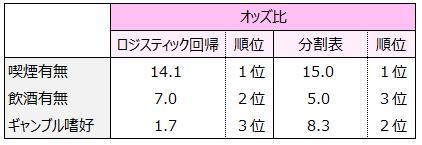
ギャンブル嗜好の順位をみると、ロジスティック回帰では3位、分割表では2位です。どちらの結果も事実ですが、統計学の世界では前者の順位を「真」、後者の順位を「偽」と考えます。後者が「偽」となる理由を次の図で考えてみます。
下記は項目間の相関係数を示したものです。
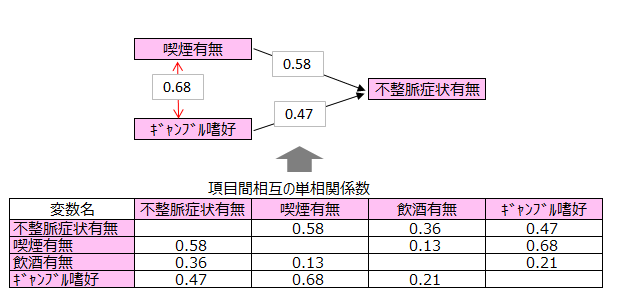
喫煙するからギャンブルが好きなのか、ギャンブルが好きだから喫煙するのか因果関係の方向は分かりませんが、両者には強い関係が見られます。
ギャンブル嗜好と不整脈症状の相関が0.47と高いのは、ギャンブル嗜好が喫煙有無の影響(相関0.68)を受けているからだと考えられます。
このことから、ギャンブル嗜好と不整脈症状は見かけの相関(偽)と考えます。
そのため、ギャンブル嗜好と不整脈症状との真の相関関係を調べることになります。真の相関関係とは喫煙有無の影響を除去した関係のことです。
これを解決してくれる解析手法がロジスティック回帰です。
ロジスティック回帰のギャンブル嗜好のオッズ比は、他要因(喫煙有無)の影響を除去して算出され、順位は3位となりました。
ロジスティック回帰の関係式の算出方法
不健康有無のデータの目的変数を0と1のデータに変更し、判別スコアを再掲します。
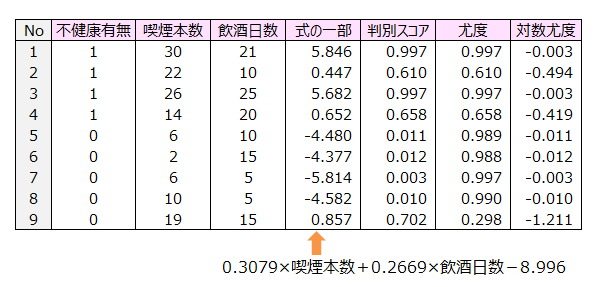
・判別スコアから尤度(尤もらしい度合い)を求めます。
不健康ある人の尤度=判別スコア ⇒不健康になる確率を表す。
不健康ない人の尤度=1-判別スコア⇒不健康にならない確率を表す
・対数尤度を求めます。
0.997の対数尤度はlog(0.997)
Excelの関数 『=LN(0.997)』を入力し、 Enterキーを押す
・対数尤度の合計を算出します。
対数尤度の合計 -2.168
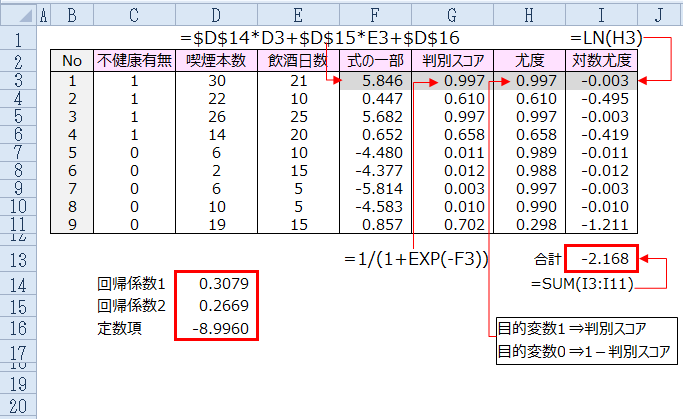
ロジスティック回帰の回帰係数は対数尤度の合計が最大になるときの値です。
対数尤度が最大となる回帰係数を求める方法を最尤法といいます。
上記画面で回帰係数、定数項は分からないとして、ブランクにします。
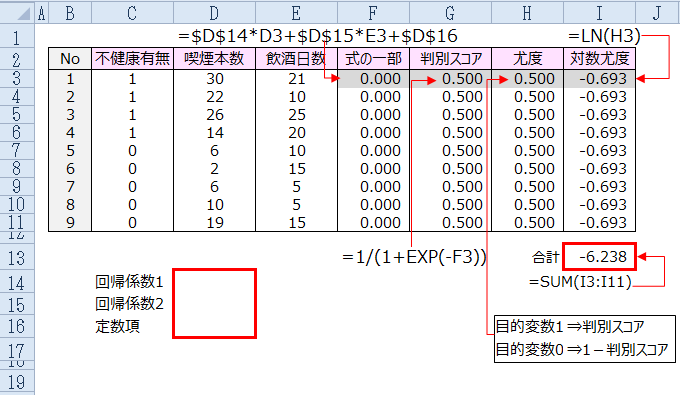
最尤法はExcelのソルバーで行えます。
Excelメニューバーの「データ」を選択すると次が表示されます。
ソルバーを選択すると次の指定画面が表示されます
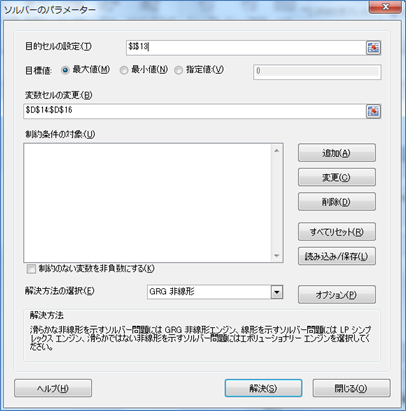
[解決]ボタンをクリックすると、結果が出力されます。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










