ロジスティック回帰
《ロジスティック回帰（１/４） 》
ロジスティック回帰分析とは
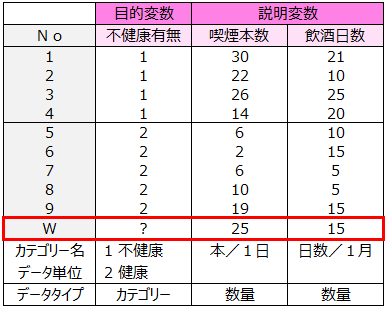
すでに確認されている「不健康」のグループと「健康」のグループそれぞれで、１日の喫煙本数と1ヵ月間の飲酒日数を調べました。下記に9人の調査結果を示しました。
下記データについて不健康有無と調査項目との関係を調べ，不健康であるかどうかを判別するモデル式を作ります。このモデル式を用い、1日の喫煙本数が25本、１ヵ月間の飲酒日数が15日であるＷさんの不健康有無を判別します。
≪例題1≫
この問題を解いてくれるのがロジスティック回帰分析です。
予測したい変数、この例では不健康有無を目的変数といいます。
目的変数に影響を及ぼす変数、この例では喫煙有無本数と飲酒日数を説明変数といいます。
ロジスティック回帰分析で適用できるデータは、目的変数は2群のカテゴリーデータ、説明変数は数量データです。
ロジスティック回帰は、目的変数と説明変数の関係を関係式で表します。
この例題の関係式は、次となります。
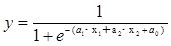
関係式におけるa1 、a2 を回帰係数、a0 を定数項といいます。
e は自然対数の底で、値は2.718 ･･･です
ロジスティック回帰分析はこの関係式を用いて、次を明らかにする解析手法です。
① 予測値の算出
② 関係式に用いた説明変数の目的変数に対する貢献度
ロジスティック回帰分析と似ている多変量解析に判別分析があります。
・判別分析について
判別分析をご覧ください。
判別分析をご覧ください。
・判別分析を行った結果を示します。
関数式：不整脈症状有無＝0.289×喫煙本数＋0.210×飲酒日数－7.61
判別得点
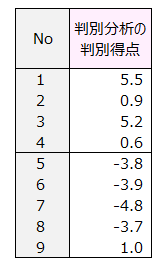
判別スコアと判別精度
関係式に説明変数のデータをインプットして求めた値を判別スコアといいます。
判別スコアの求め方をNo.1の人について示します。
関係式にNo.1の喫煙本数、飲酒日数を代入します。
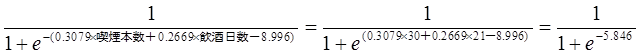
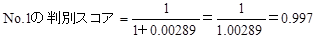
全ての人の判別スコアを求めす。
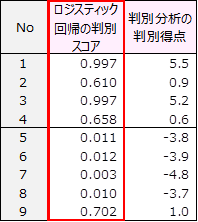
この例題に判別分析を行い、判別得点を算出しました。
両者の違いを調べてみます。
判別スコアは0～1の間の値で不健康となる確率を表します。
判別得点はおよそ－5～＋5の間に収まる得点で、プラスは不健康、マイナスは健康であることを示しています。
健康群のNo.9の人について解釈してみます。
判別スコアは0.702で、健康群なのに不健康となる確率は70.2％でした。
判別得点は1.0で、健康群なのに不健康だと判定されます。
判別精度
ロジスティック回帰における判別度は、判別的中率と相関比があります。
●判別的中率
各個体について判別スコアが0.5より大きいか小さいかでどちらの群に属するかを調べます。 この結果を推定群、不健康群と健康群を実績群と呼ぶことにします。各個体の実績群と推定群を示します。
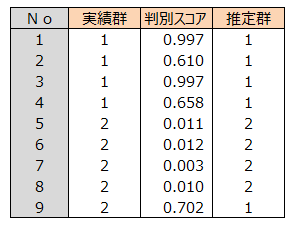
実績群と推定群とのクロス集計表（判別クロス集計表という）を作成し、 実績群と推定群が一致している度数、すなわち、「実績群1 かつ推定群1」の度数と「実績群2 かつ推定群2」の度数の和を調べます。 判別的中率はこの和の度数の全度数に占める割合で求められます。
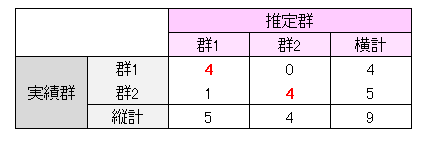
判別的中率は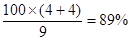
となります。
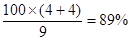となります。判別的中率はいくつ以上あればよいという統計学的基準は有りませんが, 著者は75 ％ 以上あれば関係式は予測に適用できると判断しています。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング＆マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。
