《因子分析(2/3) 》
3.因子分析の関係式
数学、英語の得点と因子得点との関係
因子分析の関係式について調べてみます。
下記に数学と英語の成績を示しました。
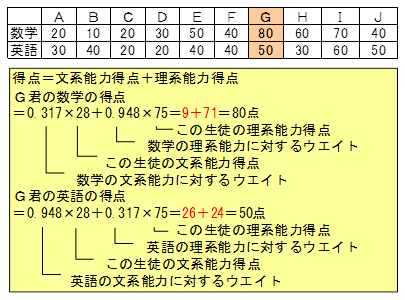
数学という科目は理系能力だけでなく文系能力も、逆に英語は文系能力だけでなく理系能力も要求されるはずです。そこで、例えば数学という科目の得点を下記図に示すように分解できないかと考えます。
この式における文系能力得点は、数学の文系能力得点に対するウエイトと、その生徒の文系能力得点との積で表されると考えます。理系能力得点も同様に、数学の理系能力に対するウエイトと、その生徒の理系能力得点との積で表されると考えます。
因子分析は下記に似示すように、ある科目の得点がいくつかの能力に分解できるという仮説をたてて、この関係式のウエイトや能力得点を求めることを目的とするものです。
この関係式のウエイトが因子負荷量、各人の能力得点が因子得点です。
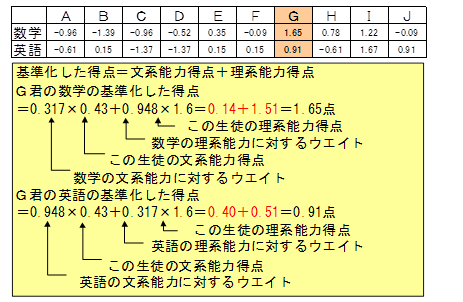
基準化した得点を能力別得点に分解
実際には、基準値にしたデータについて因子分析は行われます。
下記に示すウエイトが因子負荷量、各人の能力得点が因子得点となります。
因子分析は基準化した得点を能力別得点に分解する手法だと言えます。
4.主成分分析は合成の分析、因子分析は分解の分析
因子負荷量、因子得点の求め方の考え方をお話しします。
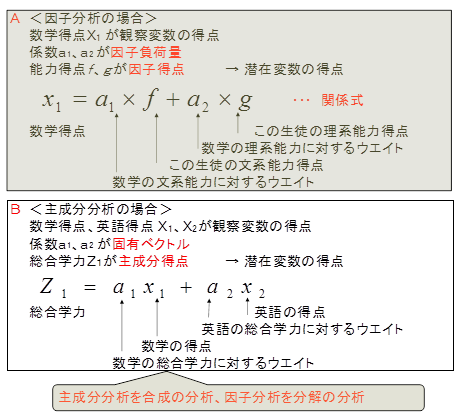
この例における英語の得点を、下記画面Aに示す記号で表してみます。
ここで、主成分分析の主成分の式を思い出してください。主成分分析では下記画面Bに示すように、各科目の得点を合成して、総合力の得点を作成しています。これに対し因子分析は、Aに示すように、ある科目の得点をいくつかの能力に分解しています。このようなことから、主成分分析を合成の分析、因子分析を分解の分析という人もいます。
共通性
前の関係式をみてください。Bの主成分分析の場合、関係式の右辺はa1、a2 が未知数でx1、x2 が既知数です。これに対しAの因子分析の場合、関係式の右辺は全て未知数です。どの多変量解析も関係式の係数は連立方程式によって求められます。因子分析のように未知数が多すぎると方程式が解けません。
既知情報を増やせば解法できるので、因子分析は次に示す方法で既知情報を増やし方程式を解き、因子負荷量と因子得点を求めています。
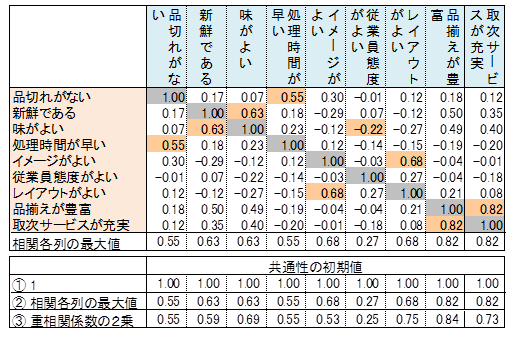
225ページのB表で共通性の結果を示しました。共通性は因子負荷量の2乗和です。「品揃えが豊富」で計算例を示すと、0.99×0.99+0.12×0.12+(-0.04)×(-0.04)+0.05×0.05=1.00 です。
因子負荷量は未知ですが共通性を既知とすれば一挙に既知情報が増え、方程式は解法できます。
共通性を決めるのは分析者、すなわちあなたです。あなたはとりあえず共通性の値はこのくらいだろ言う数値を定めます。その数値で因子分析を行い、因子負荷量を求めます。因子負荷量が求まれば共通性が計算されます。その共通性で再度因子分析を行います。このことを繰り返し行うと共通性はある一定の値に近づいて行きます。これ以上因子分析を行っても共通性の値は変わらないというところで因子分析をストップし、最終の結果を求める因子負荷量、因子得点とします。
最初に定める共通性を共通性の初期値といいます。因子分析を何回も繰り返すことを反復推定といいます。
反復推定は大変な作業と思われますが、全てコンピュータが計算してくれます。あなたがするのは共通性の初期値を定めるだけです。定めろと言われても難しく、次の3つのいずれかの値を選択することになります。
① 共通性の初期値:1
② 共通性の初期値:相関行列の各列の最大値
③ 共通性の初期値:重相関係数の2乗
当該変数をY、他変数をXとした重回帰分析の決定係数
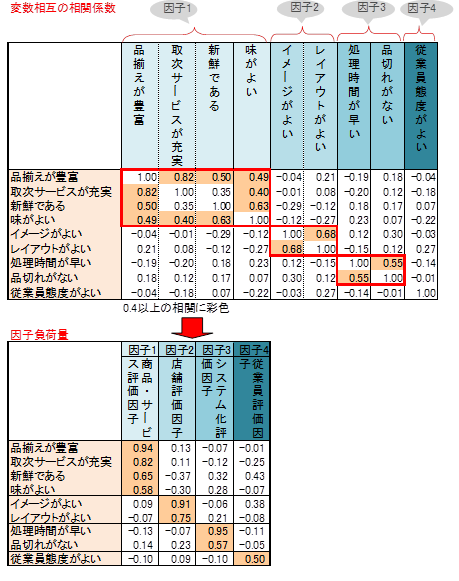
変数相互の相関係数と因子負荷量の関係
方程式によって求められた因子負荷量は変数相互の相関を集約しています。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










