《共分散構造分析(4/7) 》
GFIの大きさが1位の9番目パス図と2位の8番目パス図を示します。
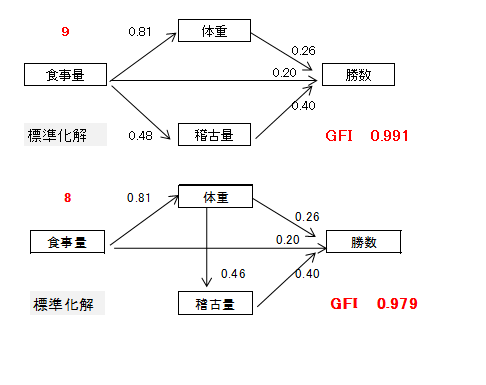
例題1の仮説は8番目パス図でしたが、繰り返し共分散構造分析をした結果、9番パス図が最適であることがわかりました。
9番目パス図(標準化解)を解釈します。
・ 食事量を増やすと体重や稽古量が増えます。
・ 体重、食事量、稽古量が多いと勝数が増える傾向がみられますが、
とりわけ稽古量の影響が大きいといえます。
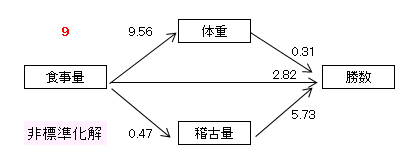
9番目パス図(非標準化解)を解釈します。
・ 食事量を1段階増やすと体重は9.56kg増えます。
・ 食事量を1段階増やすと稽古量は0.47段階増えます。
・ 食事量を一定としたとき、体重が1kg増えると勝数は0.31勝増えます。
・ 食事量を1段階増やすと勝数は2.82勝増えます。
・ 食事量を一定としたとき、稽古量を1段階増やすと勝数は5.73勝増えます。
潜在変数があるパス図
今までの例題は、観測変数のデータを用いてパス図を作成しました。ここでは潜在変数を含んだパス図について説明します。
潜在変数を導く解析手法に因子分析があります。
因子分析には、探索的因子分析と検証的因子分析がありますが、因子分析は探索的因子分析です。共分散構造分析における潜在変数は検証的因子分析によって導かれます。
探索的因子分析と検証的因子分析の違いをパス図で示すと、観測変数から潜在変数への矢印は、探索的因子分析は全ての組み合わせに、検証的因子は一部分の組み合わせに引かれています。
例題2において、総合評価を除いた9つの項目に因子分析を行い、探索的因子分析のパス図を作成すると次になります。
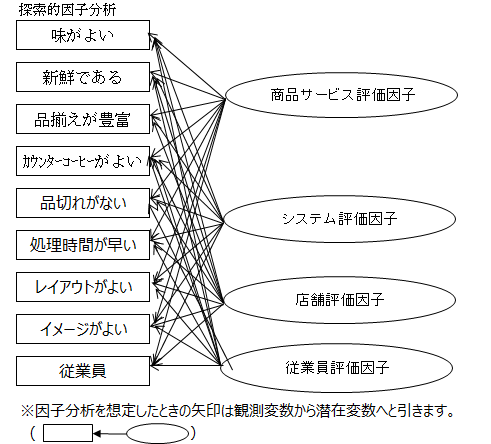
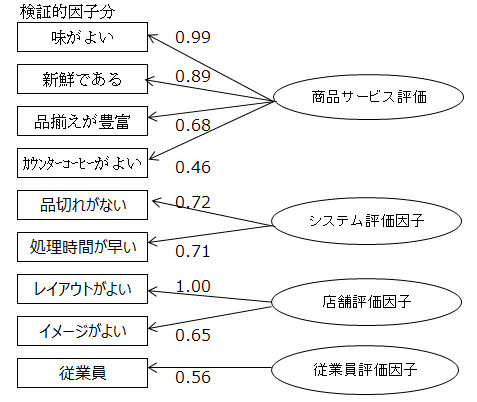
検証的因子分析のパス図を示します。
探索的因子分析は、因子がどの観察変数に影響を及ぼすかを仮定せず、どのような因子があるかを探す方法です。
検証的因子分析は、因子と観測変数を結ぶ矢印を全て引くのでなく、仮説に基づいて引いた矢印が妥当であるかを検証する方法です。具体的には商品サービス評価因子は「味がよい」「新鮮である」「品揃えが豊富」「カウンターコーヒーがよい」に影響し、他の5つの観測変数に影響を及ぼさない、「従業員評価因子は、『従業員』のみに影響している」という仮説を検証します。
パス係数は-1から1の間の値です。
マイナスの値、プラス0~0.4の値があると、その観測変数は矢印を引いた因子に属さないと判断し、矢印を引き直し共分散構造分析をやり直します。上記のパス図のパス係数は全て0.4以上です。(0.4は統計的基準ではありません)
・潜在変数の役割
・潜在変数を導入することによって、潜在変数と項目との間の因果関係を解明します。
【例】コンビニ店舗運営の仕組みであるシステム評価因子は、「品切れがない」「処理時間が早い」に影響を及ぼしています。
【例】コンビニ店舗運営の仕組みであるシステム評価因子は、「品切れがない」「処理時間が早い」に影響を及ぼしています。
・潜在変数を導入することによって多数の質問項目をまとめ、集約できます。
【例】9つの項目を4つの因子に集約します。
【例】9つの項目を4つの因子に集約します。
・潜在変数から、類似した傾向を示す項目をまとめることができます。
【例】「味がよい」「新鮮である」「品揃えが豊富」「カウンターコーヒーがよい」は回答のされ方が類似しており、商品サービス評価因子としてまとめることができます。
【例】「味がよい」「新鮮である」「品揃えが豊富」「カウンターコーヒーがよい」は回答のされ方が類似しており、商品サービス評価因子としてまとめることができます。
・潜在変数の間で因果関係を検討すれば、多くの項目の間の関係を直接扱うより効率が良くなります。
【例】上記のパス図は因子間の相関は無いとして、因子間の矢印は引かれていません。商品サービス評価因子と店舗評価因子の関係を見たければ、両因子を矢印で結びます。商品サービス評価因子の項目数は4つ、店舗評価因子の項目数は2つです。前者4項目と後者2項目の関係をみるより、商品サービス評価因子と店舗評価因子の関係を見る方が、効率が良くなります。
【例】上記のパス図は因子間の相関は無いとして、因子間の矢印は引かれていません。商品サービス評価因子と店舗評価因子の関係を見たければ、両因子を矢印で結びます。商品サービス評価因子の項目数は4つ、店舗評価因子の項目数は2つです。前者4項目と後者2項目の関係をみるより、商品サービス評価因子と店舗評価因子の関係を見る方が、効率が良くなります。
・重回帰分析を行う場合、項目間に高い相関があると、係数の符号逆転現象(マルチコ)が発生します。潜在変数間に無相関を仮定し、これら潜在変数を説明変数とすれば符号逆転現象は起こりませえん。
【例】例題2は4つの因子を説明変数、総合評価を目的変数として重回帰分析を共分散構造分析でしたということです。総合評価への影響度は、商品サービス評価因子が最も高く、次にシステム評価因子、従業員評価因子が続きます。店舗評価因子の影響度はほとんどないといえます。
【例】例題2は4つの因子を説明変数、総合評価を目的変数として重回帰分析を共分散構造分析でしたということです。総合評価への影響度は、商品サービス評価因子が最も高く、次にシステム評価因子、従業員評価因子が続きます。店舗評価因子の影響度はほとんどないといえます。

共分散分析の解析手順
≪例題3≫
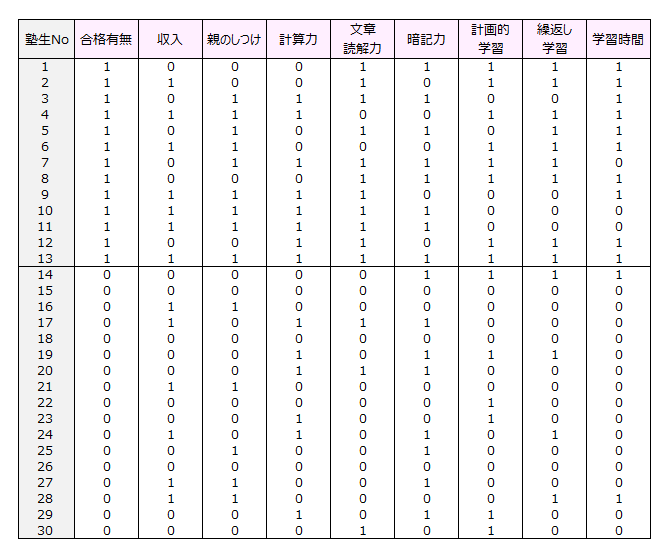
大学受験進学塾で、有名校T大学に合格した13人と不合格の17人を対象に、アンケート調査を行いました。
塾生の家庭環境、学習方法、知的能力と合格有無との因果関係を明らかにしてください。
質問文を示します。

回答データを示します。
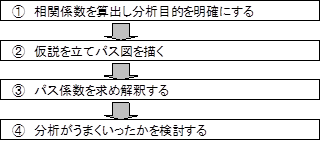
共分散構造分析の解析手順を示します。