《コンジョイント分析 (3/3)》
2.コンジョイント分析の計算方法と結果の見方
コンジョイント分析が適用できるデータ形態(1)
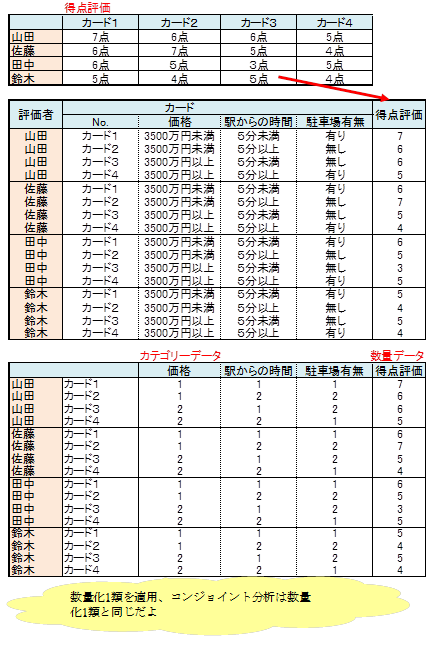
4人の評価結果を、右の表に記載しました。
下記のカテゴリーデータの表は、カテゴリー名をカテゴリーコードに置換したものです。
この表を多変量解析に適用するデータとします。このデータの個体数、変数のデータ形態を調べました。
個体数は16(4人×4枚)です。目的変は得点評価で数量データです。説明変数は価格、駅からの時間、駐車場有無でカテゴリーデータです。
このデータに適用できる多変量解析は数量化1類です。
コンジョイント分析が適用できるデータ形態(2)
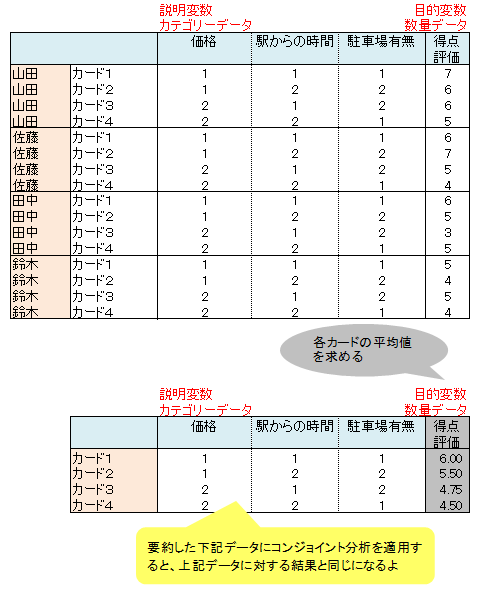
右の表はカードごとの平均値を求めました。
上表、下表に数量化1類を適用します。両者の結果は一致します。このケースだけでなく、いま述べた方式で作られるデータはどのような場合も一致することがわかっています。
コンジョイント分析データに数量化1類を適用
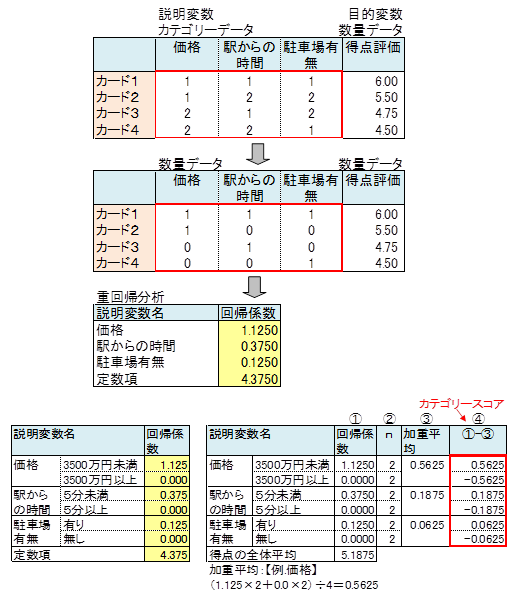
数量化1類は重回帰分析とほぼ同じです。したがって、数量化1類のソフトがなくても、Excelの分析ツールにある回帰分析で数量化1類を処理できます。
カードごとの平均を求めた表に重回帰分析を適用します。ただしカテゴリーデータは1,0データに変換してから重回帰分析を実行します。
重回帰分析より得られた結果を重回帰分析のカテゴリースコアの求めかたの手順に従い、カテゴリースコアを求めました。下表の④がカテゴリースコアです。
コンジョイント分析の結果
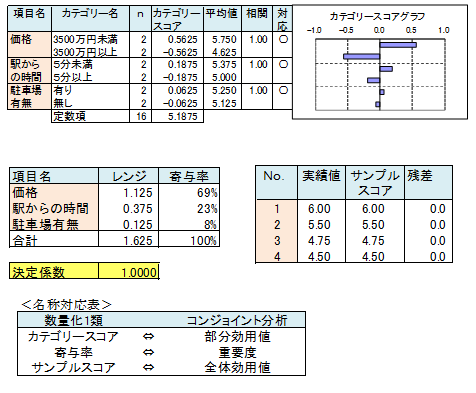
数量化1類の結果示します。
数量化1類で出力された結果を、コンジョイント分析では別の名称で表記します。
カテゴリースコアを部分効用値、寄与率を重要度、サンプルスコアを全体効用値といいます。
コンジョイント分析の結果の見方
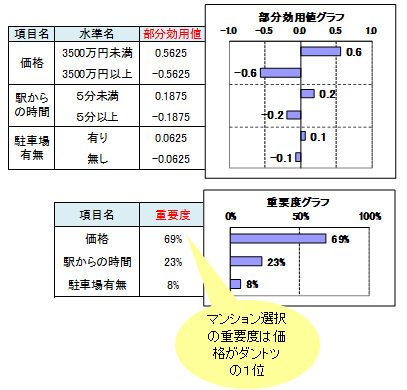
部分効用値は棒グラフで示すのが一般的です。棒グラフから次の解釈ができます。
価格という商品特性において3500万円未満という水準は、マンション総合評価を0.6点高める役割を果たし、全水準の中で最も高い貢献度となりました。逆に3500万円以上の水準はマンション総合評価を0.6点低め、全水準の中で最も低い貢献度となりました。
同様に駅からの時間についてみると、5分未満は0.2点の貢献度、5分以上は-0.2点の貢献度でした。駐車場有無は、有りは0.1点、無しは-0.1点の貢献度でした。
値がプラスの部分効用値に着目し、マンション総合評価を高めるのに貢献する水準は、価格3500万円未満、駅からの時間5分未満、駐車場有りであるという、言い方もできます。
重要度は棒グラフで示すのが一般的です。棒グラフから次の解釈ができます。
マンションの選択(購入)において最も重要な商品特性は価格で、次に駅からの時間であることが分かります。駐車場の有無は10%を割り、それほど重要でないことが分かりました。
カードごとに4人の得点の平均を算出します。これをカード別平均得点と名称します。カード別平均得点と全体効用値との単相関係数を重相関係数といいます。重相関係数の2乗を決定係数といいます。
決定係数が高いほど分析精度はよいといえます。
マンションの例はカード別平均得点と全体効用値が一致しているので決定係数は1になりました。
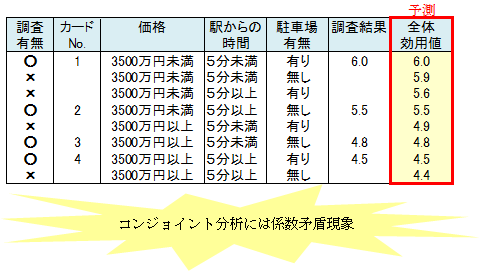
分析精度が高い場合は、調査しなかったカードの評価得点が予測できます。
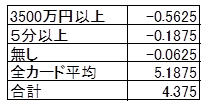
カードNo.8について予測します。このカード商品特性の水準は、3500万円以上、5分以上、無しです。この水準の部分効用値と評価得点の全カード平均値を加算します。
コンジョイント分析データに数量化1類を適用した説明変数は、直交表の水準値を適用したものです。
直交表は、表内の任意の2列の単相関係数を計算すると必ず0になるといいました。
係数矛盾現象は説明変数相互の相関が高いときに起こる現象なので、コンジョイント分析は説明変数が直交表のデータであることから「係数矛盾現象」は起こりません。

アンケート分析をおこなお うと考えている方, そして 分析業務をすでに実務でさ れている方のための入門書 籍です。 初級編、中級編、上級編に 分かれているため、自己の のレベルに合わせて読むこ とができます。 分析レポート編として、5 つ のレポートを紹介していま す。
著 者:菅 民郎
出版社:オーム社
価 格:2,808円
体 裁:B5変形判 389頁
出版年月:2007年9月26日







