《主成分分析(3/4) 》
関係式の係数/固有ベクトルの求め方
関係式の係数、すなわち固有ベクトルはどのような考え方で導かれるかを考えてみます。考え方は二つあります。
<1番目の考え方>
総合タレント力を算出する関係式の係数は、タレントとしての基本的技能ほど重要と考え高い値となります。歌唱力がなければ瞬間芸、ものまね、踊りも上手になれないので歌唱力は重要だということです。容姿は他の科目にあまり影響を与えないので重要でないということです。
観測変数相互の相関係数を算出したとき、どの科目とも相関の高い、すなわち相関係数の横計が大きい科目ほど重要だといえます。
横計と第1主成分の固有ベクトル(総合タレント力)と対比させると順位は一致しています。
だからといって、固有ベクトルの計算は相関の横計から算出しているわけではありません。あくまで考え方です。
系別能力を算出する関係式の係数は次の考え方から導かれることが推察できます。
観測変数相互の相関を調べると、瞬間芸が上手い人はものまねが上手い、踊りの上手い人は容姿がよいといった傾向がみられ、人の能力はおおざっぱに捉えると、お笑い系能力とアイドル系能力に大別できそうということが読み取れます。
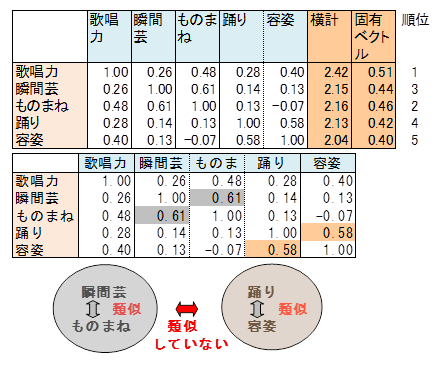
このようにして求められた距離を系別能力と考えます。この例では、Z2のプラス方向が文系能力、マイナス方向が理系能力と推察できます。
<2番目の考え方>
ここでは簡単な例で、関係式の係数がどのようにして求められるかを考えてみます。右は10人の生徒の数学と英語の成績(10点満点)を示したものです。
英語を縦軸に、数学を横軸にとり、散布図を作成します。数学と英語の重心(平均)を通り、散布点の真ん中を通る直線(Z1)を引きます。直線Z1に各点から垂線をおろし、重心からその点までの距離を求めます。ただし、重心より左側の点の距離にはマイナスを付けます。Gの距離は4.0、Bは-2.9となります。数学、英語の点が高く、図では右上に位置するGの値が最大、英語は平均点とほぼ同じだが数学の点が最も低いBの値が最小となりました。
このようにして求められた距離を総合力と考えます。総合力は、2つの観測変数(数学と英語)で測定された得点を、1つの直線上の距離で表したということです。
重心を通り、Z1に垂直な直線Z2を引きます。直線Z2に各点からの垂線をおろし、重心からその点までの距離を求めます。ただし、重心より下側の点の距離にはマイナスを付けます。Gの距離は-0.4、Bは1.4です。Gは数学も英語も平均点を上回っていますが、数学の方が英語より点が高いので、Z2の直線上ではマイナスの値となりました。Bは英語の方が数学より点が高いので、Z2の直線上ではプラスの値となりました。Z2は総合力がある、ないに関わらず、数学と英語の点のどちらが高いかによって作られています。
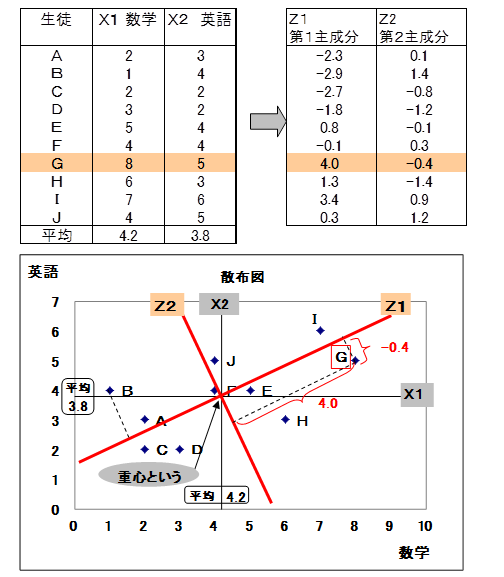
X1とX2が観測変数で、Z1とZ2が主成分(潜在変数)です。
X1とX2で作られる平面上の座標を(x1,x2)、Z1とZ2の平面上の座標を(z1,z2)とします。Gで示すと(x1,x2)=(8,5)、(z1,z2)=(4.0,-0.4)です。
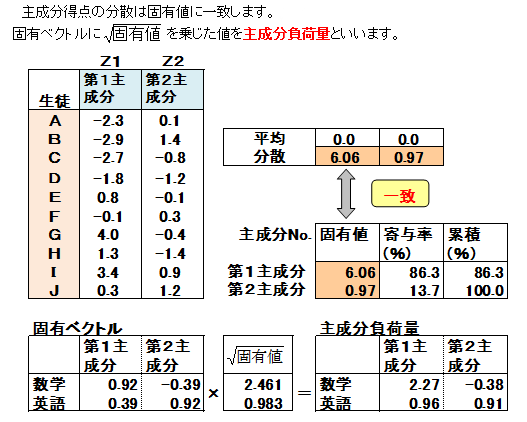
下記はこのデータに対する主成分分析の結果です。
この式にGのx1=8、x2=5の値を代入すると、
Z1= 0.9215×8+0.3884×5=9.3
Z2=-0.3884×8+0.9215×5=1.5
この式に重心のx1=4.2、x2=3.8の値を代入すると、
Z1= 0.9215×4.2+0.3884×3.8=5.3
Z2=-0.3884×4.2+0.9215×3.8=1.9
Gの重心までの距離、すなわち座標(z1、z2)を求めると、
z1=9.3-5.3=4.0
z2=1.5-1.9=-0.4
主成分分析の関係式、固有ベクトルは、観測変数軸X1、X2の座標を主成分軸Z1、Z2の座標を求めるためのものでした。
理解するのが難しかったと思いますが一言でいうならば、関係式の係数は観測変数の座標を潜在変数の座標に変換するためのツールだということです。
<補足>
主成分分析のパソコンソフトによる結果の見方
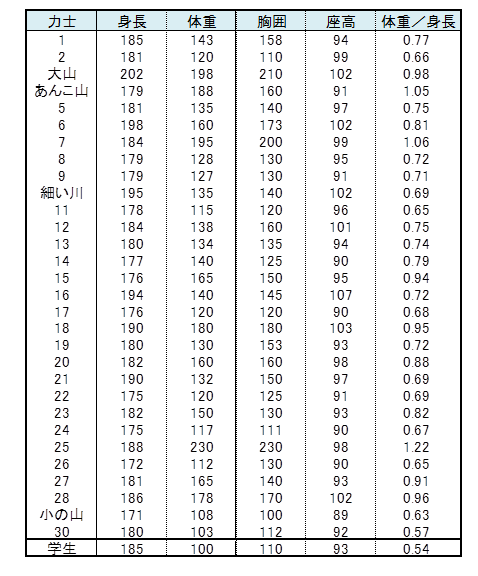
右の表は、大相撲の力士30人における身長、体重、胸囲、座高を示したものです。5番目の変数は、体重を身長で割った値です。相関行列による主成分分析を行い、力士の体型を調べる潜在変数を二つ見出し、その潜在変数で作られる平面上に力士をポジショニングしなさい。
学生横綱であるW君の主成分得点を計算し、大相撲の力士と体型を比較しなさい。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。










