
直線回帰分析について学ぶ
第4話は、雪乃が少しではあるが統計解析に自信を持った時、常夏市環境課の担当者から受けた依頼がテーマである。
依頼主: 「こんにちは。常夏市環境課の佐藤です。」
雪乃: 「統分雪乃です。よろしくお願いします。」
佐藤: 「早速ですが、お願いしたいテーマをお話しします。
我が常夏市の8月の平均気温は、過去30年で3度の上昇がみられ、他の都市に比べて大きな上昇です。
気温上昇の原因には、地球温暖化の影響もありますが、ヒートアイランド現象を含む都市温暖化の傾向が、顕著に現れています。
何も対策をたてずにいると、この傾向が増加し30度ラインを超えてしまうことを、市議会に提示したいと思います。
お願いしたいことは、常夏市の10年後の平均気温がどうなるかを推計していただくことです。」
雪乃: 「常夏市の気温データをいただけますか。」
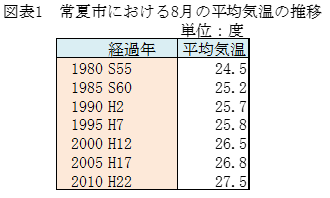
佐藤: 「こちらのデータでよろしいですか。」
(図表1参照)
雪乃: 「はい、このデータから2015年と2020年の8月の平均を推計させていただきます。結果がでましたらご連絡させていただきます。」
この案件については、雪乃は1人で分析しようと思ったが、結局は所長の力を借りながら分析することになった。

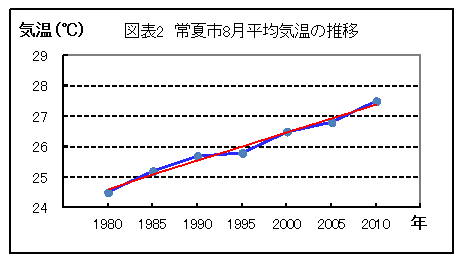
雪乃: 「縦軸(Y軸)を平均気温、横軸(X軸)を経過年にとり、折れ線グラフを描きました。そして折れ線グラフの真ん中を通る直線を引きました。」(図表2参照)
所長: 「そしてどうしたの?」
雪乃: 「この直線の傾向通りに平均気温が推移するとすれば、2015年、2020年の平均気温はこの直線上にあるということで、次のようにして2015年、2020年の平均気温を求めました。」(図表3参照)
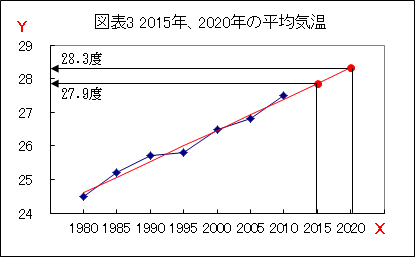
所長: 「予測値を求める考え方はよいけど、直線の引き方に疑問を感じるね。」
雪乃: 「やっぱり、真ん中を通る直線を適当に引いたのはまずいですね。」
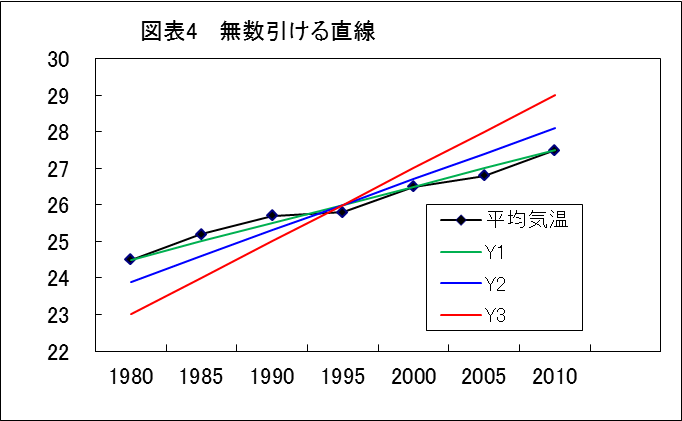
所長: 「そうだ。図表4のように直線は引こうと思えば何本でも無数に引けるよね。どの直線が良いか理論的に説明できないとお客様は納得しないよ。」
所長: 「図表5に示すように、点から直線「Y3」までの差を計算し、その2乗を求めるんだ。」
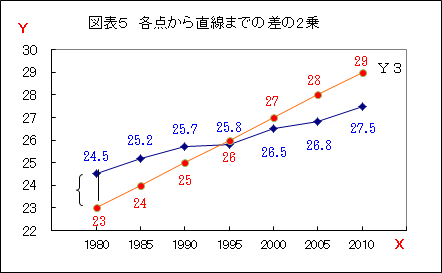
雪乃: 「分かりました。(カチカチカチ・・)
全ての点について、直線「Y3」との差の2乗を求めました。」(図表6参照)
所長: 「差の2乗の合計はいくつかな。」
雪乃: 「8.16です。」
所長: 「この値を残差平方和というんだ。」
雪乃: 「残差平方和を計算するとき、なぜ差の2乗をするんですか。」

所長: 「差の合計だと、いかなる場合も0になるので、残差平方和は差の2乗の合計なんだ。」
雪乃: 「なるほど、よく分かりました。」
所長: 「他の直線Y1、Y2についても残差平方和を求めてください。」
雪乃: 「求めました。」(図表7,8参照)
所長: 「残差平方和が最小となる直線はどれかな。」(図表9参照)
雪乃: 「Y1です。」
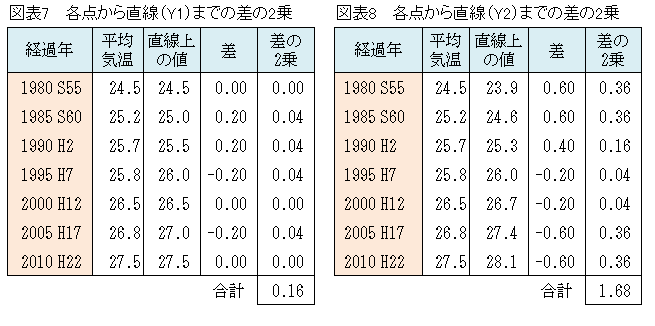

所長: 「【図表4 無数引ける直線】と【図表9 各直線の残差平方和】と突き合わせて見てください。平均気温の各点が直線に近いのはY1だ。このY1の残差平方和が最も小さいよね。」
雪乃: 「はい、その通りです。」
所長: 「残差平方和が最小となる直線が最適な直線といえるんだ。」
雪乃: 「分かりました。」
所長: 「このような考え方で直線を導く方法を、最小二乗法というのだ。」
雪乃: 「考え方はわかりましたが、いくつもの直線について残差平方和を求めるのは大変な作業になります。もっと簡単な方法で直線を求める方法はないのでしょうか。」
所長: 「あるよ」
雪乃: 「(もぉう~それなら最初から教えてくれればいいのにと思いつつ)教えてください。」
所長: 「図表1においては、経過年が決まれば平均気温がピッタリ決まるという関係が見られない。だから経過年と平均気温の関係を、関係式で表すことはできないんだ。」

統計探偵物語
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。









