リスク比とオッズ比
◆リスク比とオッズ比(3/4)◆
3. オッズ比の使い道
「2.よくあるオッズ比の間違った解釈」では、オッズ比でよく誤解される使い方やオッズ比の解釈を学習しました。読者の皆さんの中には、オッズ比の使い道があまりないのではないか、と考えてしまう方もいるかもしれません。
確かにリスク比に比べ、オッズ比は理解しにくいのですが、実際には臨床研究でもよくみるのがオッズ比です。
それでは、事例に沿って説明をしていきましょう。
不整脈になる要因はいろいろありますが、ここでは仮に、喫煙の有無、飲酒の有無、性別を取り上げ、どの要因が不整脈の有無に影響を及ぼしているかを調べることにします。
表8は、それぞれの要因についての分割表、リスク比、オッズ比を示したものです。
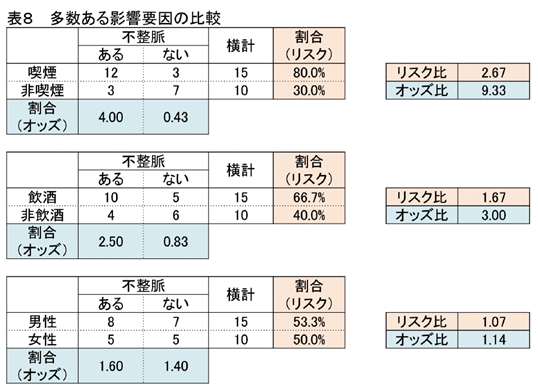
次に、リスク比の順位はどうなっているでしょうか?
値が高い順からみてみましょう。喫煙の有無が2.67で1位、飲酒の有無が1.67 で2位、性別が1.07 で3位となります。
では、オッズ比の順位はどうなっているでしょう?
喫煙の有無は9.33、飲酒の有無は3.00、性別は1.14 で、順位はリスク比と同じです。
つまり、不整脈に影響を及ぼす要因の順位は、リスク(割合)の差、リスク比、オッズ比、どれを用いても把握できるということになります。リスク比、オッズ比どちらを使っても、不整脈の影響要因の1位は喫煙の有無、2位は飲酒の有無ということになります。
リスク比のほうが使いやすいので、リスク比で解析することも多いのですが、臨床研究ではオッズ比を用いる人のほうが多いように思います。それは、影響要因の順位がわかれば目的を達成できるからでしょう。なお、オッズ比は順位の把握だけなので、オッズ比を使う場合は有意差検定が必須になります。
リスク比とオッズ比について、一度、今までの内容をまとめてみましょう。

これらをひと言でまとめると、オッズ比は、複数の影響要因の寄与順位を把握することのみに活用でき、リスクの倍率把握には適用できない、ということになります。
理解しづらい「逆相関」を理解しやすくする方法
下記の表9の分割表のリスク比、オッズ比をみてみましょう。表8との違いがおわかりになるでしょうか?
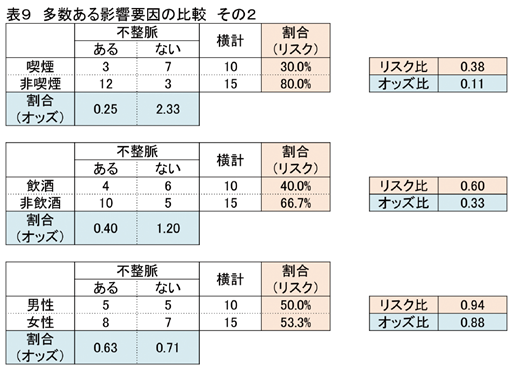
表9は、喫煙と非喫煙のデータを入れ替えて表にしています。
飲酒と非飲酒、男性と女性も同様です。
表9の一番上の表について、どのように解釈できるのか説明していきましょう。
リスク(割合)は、喫煙者の方が非喫煙者に比べて小さくなっています。
喫煙者が不整脈になるリスクは30%で、非喫煙者のリスクは80%なので、喫煙者のほうが50%リスクが低い。
リスク比が0.38(30%÷80%)ということから、喫煙者が不整脈となるリスクは、非喫煙者に比べ0.38倍となります。
表8は「喫煙者は非喫煙者に比べ、不整脈になりやすいという事例」でした。
表9は、「(実際にはあり得ないですが)喫煙者は非喫煙者に比べ、不整脈になりにくいという事例」となります。
喫煙と不整脈の関連性をみると、表8は「喫煙あり→不整脈あり」、「喫煙なし→不整脈なし」と通常考えられる関連ですが、表9では「喫煙あり→不整脈なし」、「喫煙なし→不整脈あり」という、通常ではあり得ない関連となってしまうのです。
前者(表8)の関連を正の相関、後者(表9)を逆相関ともいいます。
これらの表からわかるように、リスク比、オッズ比どちらも、正の相関の場合は1より大きく、逆相関の場合は1より小さくなっています。
ここまでのところをまとめてみましょう。
リスク比、オッズ比ともに値が1より大きくなるほど、喫煙者は非喫煙者に比べ、不整脈になる傾向が高まるといえます。このような関連性を「正の相関関係がある」といいます。
リスク比、オッズ比とも値が1より小さくなるほど、喫煙者は非喫煙者に比べ、不整脈にならないという傾向が高まるといえます。このような関連性を「逆相関」といいます。
つまり、表8の場合、リスク比は2.67>1で正の相関、すなわち、喫煙する人ほど不整脈になりやすい。
表9の場合、リスク比は0.38<1で逆相関、すなわち、喫煙する人ほど不整脈になりにくい、ということになります。
さて、理解はできたものの、リスク比が0.38 倍というのが何か気になる、わかりにくいという方もいらっしゃるのではないでしょうか? 一般にはあり得ない表9の一番上の表の喫煙と非喫煙の位置を入れ替えた表10を作り、リスク比を計算してみましょう。
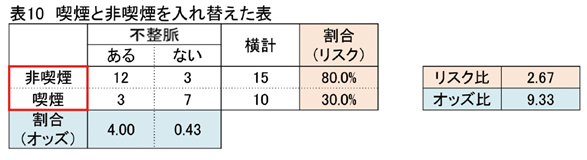
このように、リスク比は1を上回りました。リスク比を解釈するとどうなるでしょうか?
非喫煙者は、喫煙者に比べ2.67倍、不整脈になるといえます。
表9の解釈、つまり「喫煙者は非喫煙者に比べ0.38 倍、不整脈になる」と同じことになりますが、表10 の表現のほうがわかりやすくなりますね。
リスク比が1を下回った場合は、このような対応をお勧めいたします。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。









