
◆母平均の差の検定(4/6)◆
9. T値
仮説検定の3種の神器は信頼区間、T値、P値だと、前に述べました。
信頼区間の説明が終わり、次はT値の説明となります。
T値は平均値をSE(標準誤差)で割った値です。


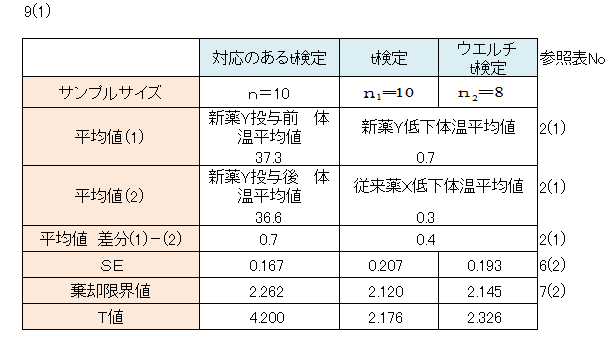
「2(1)」のデータについてT値を求めます。
T値による仮説検定
T値を算出する式に代入する平均値は、平均値の差分です。
平均値の差分が大きいということは薬剤の解熱効果あるということです。
したがってT値が大きいほど解熱効果があるということです。
母集団において解熱効果があるかいなかは、統計学が決めた基準の値とT値の比較で行えます。基準の値は先に説明した「棄却限界値」を用います。

新薬Yの低下体温の仮説検定
・データ
対応がある
・検定方法
対応のあるt検定
・帰無仮説
新薬Y投与前体温平均値と新薬Y投与後平均値は同じ
・信頼区間を求める平均値
新薬Y投与前体温平均値と新薬Y投与後体温平均値の差分(新薬Y低下体温平均値)
・検定に用いる検定統計量
T値と棄却限界値
・判定
表9(1)より T値=4.200 棄却限界値=2.262
T値>2.262
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
母集団において、新薬Yは信頼度95%で解熱効果があるといえる。
新薬Y低下体温平均値と従来薬X低下体温平均値の差分の仮説検定
・データ
対応がない
・検定方法
対応のないt検定
・帰無仮説
新薬Y体温平均値と従来薬X平均値は同じ
・信頼区間を求める平均値
新薬Y低下体温平均値と従来薬X低下体温平均値の差分
・検定に用いる検定統計量
T値と棄却限界値
・判定
「9(1)」より T値=2.176 棄却限界値=2.120
T値>2.120
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
母集団において、新薬Yは従来薬Xに比べ解熱効果があるといえる。
注:ウエルチt検定は割愛しました。
10. P値
仮説検定の3種の神器は信頼区間、T値、P値だと、前に述べました。
信頼区間、T値の説明が終わり、最後はP値の説明となります。
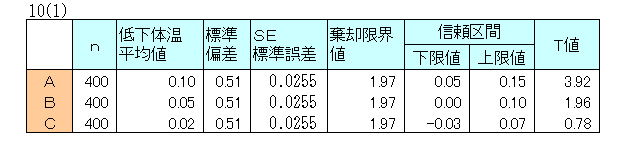
3つの薬剤A,B、Cの低下体温を調べる調査をしました。
対応のあるt検定を行い、各薬剤の信頼区間、T値を求め、母集団における効果を調べました。

次は信頼区間とT値を図にしたものです。
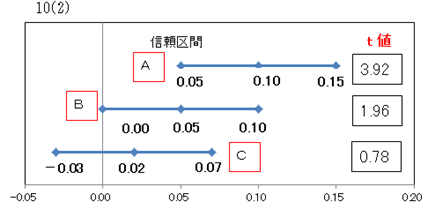
P値は信頼区間と密接な関係があります。
・P値は、Bのように下限値が0の場合はP=0.05となります。
・AはP値が0.05より小さい値、CはP値が0.05より大きい値になります。
P値はT値とも密接な関係があります。
・T値が大きくなるほどP値は小さくなるという関係があります。
P値とはprobability(確率)の頭文字です。Pの値は0~1の間の値です。
P値は仮説検定でくだした結論の間違う確率を示しています。
P値は小さくなるほど誤る確率は低くなり、母集団において効果がある(違いがある)という結論の確からしさが高まります。
3薬剤のP値は次となります。
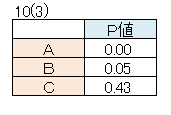
AのP値は0なので、効果があるという判断が間違う確率は0%、確からしさは100%です。
BのP値は0.05なので、効果があるという判断が間違う確率は5%、確からしさは95%です。
CのP値は0.43なので、効果があるという判断が間違う確率は43%、確からしさは57%です。
P値(間違う確率)が低ければ効果があると判断はだせますが、P値が高ければ効果があるという判断は出せません。そこで、統計学は5%という基準(有意点という)を設定ました。
P値が有意点5%より小さければ効果がある、大きければ効果なしとします。
P値は手計算で求められませんが、Excelの関数で求められます。

BについてP値を求めます。
対応のあるt検定の自由度はn-1なので、自由度=400-1=399です。
「10(2)」よりT値は1.96です。
=TDIST(1.96,399,2) 「Enter」キー P値0.05が出力される。
P値による仮説検定


新薬Yの低下体温の仮説検定
・データ
対応がある
・検定方法
対応のあるt検定
・帰無仮説
新薬Y投与前体温平均値と新薬Y投与後平均値は同じ
・信頼区間を求める平均値
新薬Y投与前体温平均値と新薬Y投与後体温平均値の差分(新薬Y低下体温平均値)
・検定に用いる検定統計量
P値と有意点
「9(1)」より T値=4.200 自由度=n-1=10-1=9
Excel関数 =TDIST(4.2,9,2) → P値= 0.00231
・判定
P値<0.05
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
母集団において、新薬Yは信頼度95%で解熱効果があるといえる。
新薬Y低下体温平均値と従来薬X低下体温平均値の差分の仮説検定
・データ
対応がない
・検定方法
対応のないt検定
・帰無仮説
新薬Y体温平均値と従来薬X平均値は同じ
・信頼区間を求める平均値
新薬Y体温平均値と従来薬X体温平均値の差分(新薬Yの低下体温平均値)
・検定に用いる検定統計量
P値と有意点
「9(1)」より T値=2.176 自由度= n1+n2 -2=10+8-2=16
Excel関数 =TDIST(2.176,16,2) → P値=0.0448
・判定 P値<0.05
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
母集団において、新薬Yは従来薬Xに比べ解熱効果があるといえる。
・判定別の仕方
P値と有意点0.5との比較で有意差判定をおこないましたが、P値そのものを使って解釈することもできます。
「母集団において、新薬Yは従来薬Xに比べ解熱効果がある」という判断が間違う確率は3.49%です。
注:ウエルチt検定は割愛しました。
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。
マーケティングプランニング&マーケティングリサーチ入門セミナー
マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。
統計解析入門セミナー
統計学、解析手法の役割から種類、概要までを学びます。
アンケート調査表作成・集計・解析入門セミナー
調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。









