
◆母平均の差の検定(2/6)◆


①「等しい」という仮説をたてる。
統計学では帰無仮説という
帰無仮説は統計学観点からたてる仮説。
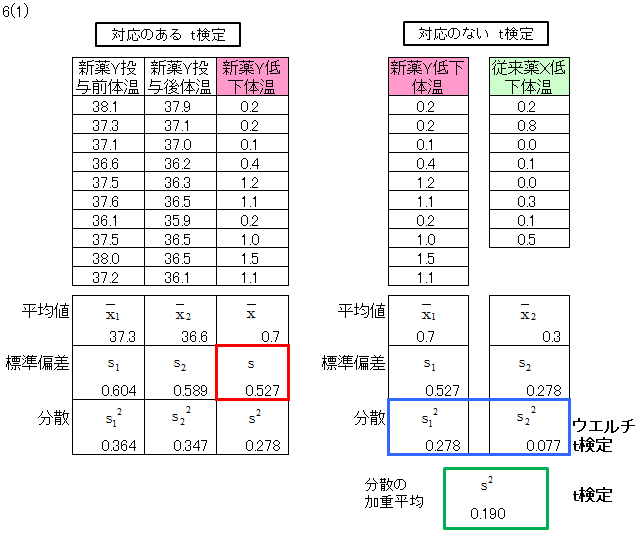
【例】母集団の「新薬Yの投与前体温平均値と投与後体温平均値は等しい」
②「異なる(解熱効果がある)」という仮説をたてる。
統計学では対立仮説という。
対立仮説は分析者が結論(目的)とする仮説。
【例】母集団の「新薬Yの投与前体温平均値と投与後体温平均値は異なる(解熱効果がある)」
方法1 信頼区間の下限値と上限値の符号が同じか異なるかを比較
方法2 T値と棄却限界値を比較。
方法3 P値と有意点を比較。(よく用いられる有意点は0.05 )
3つの方法のいずれかで行う。どの方法を選択しても結論は同じ。
<条件式が下記の場合>
方法1 下限値と上限値の符号が同じ
方法2 T値>棄却限界値
方法3 P値<有意点0.05
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
対立仮説の採択によって、母集団において、異なる(解熱効果がある)がいえる。
このことを、「信頼度95%で有意な差がある」という言い方をする。
【例】母集団の「新薬Yの投与前体温平均値と投与後体温平均値は信頼度95%で有意な差がある。」
母集団において新薬Yは解熱効果があったといえる。信頼度は95%である。
<条件式が下記の場合>
方法1 下限値と上限値の符号が異なる
方法2 T値<棄却限界値
方法3 P値>有意点0.05
「等しい」という仮説を棄却できず、「異なる」という対立仮説を採択しない。
対立仮説を採択できず、母集団において、異なる(解熱効果がある)がいえない。
このことを、「信頼度95%で有意な差があるといえない」という言い方をする。
【例】母集団の「新薬Yの投与前体温平均値と投与後体温平均値は信頼度95%で有意な差があるといえない。」
母集団において新薬Yは解熱効果があったといえない。信頼度は95%である。


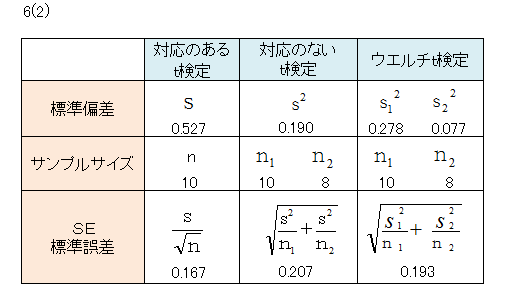
統計的推定・検定の手法別解説
統計解析メニュー
最新セミナー情報
予測入門セミナー
マーケティングプランニング&マーケティングリサーチ入門セミナー
統計解析入門セミナー
アンケート調査表作成・集計・解析入門セミナー









