相関比(２/２） :: 【公式】株式会社アイスタット

◆相関比（２/２）◆

＜級間変動＞

グループの平均を計算し、3つの平均のばらつきを算出します。年令幅が重複しないということは、3つの平均のばらつきが大きいことを、逆に年令幅が重複するということは、3つの平均のばらつきが小さいことを意味します。

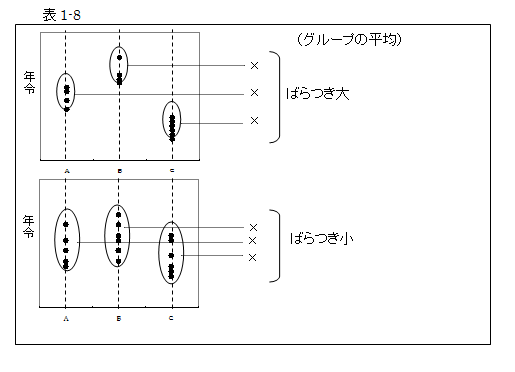
年令幅のばらつき、すなわちグループ間のばらつきは、各グループの平均と全体平均との差から求められ、これを級間変動といい、S_Bで表します。

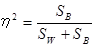
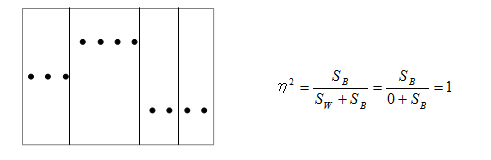
いままでの説明でお分かりのように、級内変動が小さく、級間変動が大きいとき関連があると判断します。

そこで、2つの変動合計に対する級間変動の割合を求めます。これを相関比といい

η²（イータ2乗＿と読む）で表します。

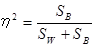
この式をみると、最も関連が強いとき、級内変動（Ｓｗ）は「0」、すなわちグループ内に属するデータが全て同じになり、η²は「1」になります。

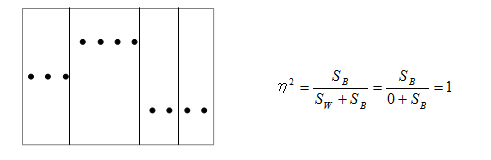
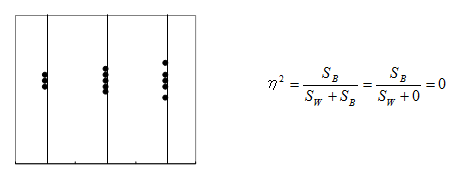
逆に、最も関連が弱いとき、級間変動（S_B）は「0」、すなわちグループ平均が全て同じになり、η²は「0」になります。

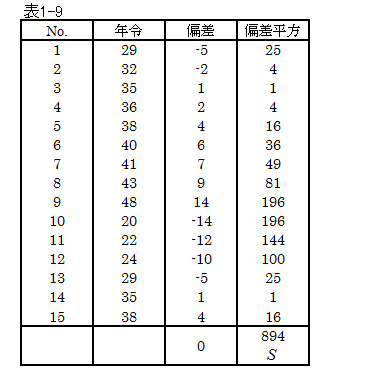
ここで、表1-1の全体の偏差平方和を求めてみます。全体平均、X =34より、次となります。

偏差平方和 S は894となります。S_Wは354、S_Bは540です。これらをくわえるとS に一致します。

S = S_W+ S_B

この例だけでなくどんな場合も一致します。したがって相関比η²は、次の公式となります。

相関比はいくつ以上あればよいか

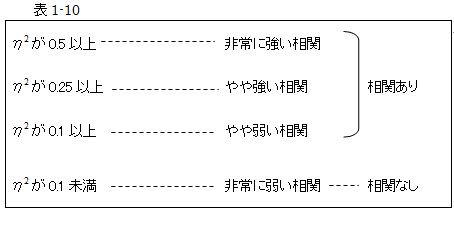
相関比は0から1の間をとり、1に近づくほど、2変数は相関関係があることが分かりました。

それでは、η²（相関比）が、いくつ以上あれば相関関係があるといえるのでしょうか。

単相関同様、基準はありません。著者は次のように定めています。

Severity: Notice

Message: Trying to get property of non-object

Filename: helpers/api_helper.php

Line Number: 191

予測のための基礎知識、予測の仕方、予測解析手法の活用法・結果の見方を学びます。

マーケティングリサーチを学ぶ上で基礎・基本からの調査のステップ、機能までをわかりやすく解説しています。

統計学、解析手法の役割から種類、概要までを学びます。

調査票の作成方法、アンケートデータの集計方法、集計結果の見方・活用方法を学びます。