時系列予測の手法別解説

HOME
>
時系列予測の手法別解説
>
EPA法（３/３）

＜＜前のページへ　　１　　２　　３

【EPA法（３/３）】

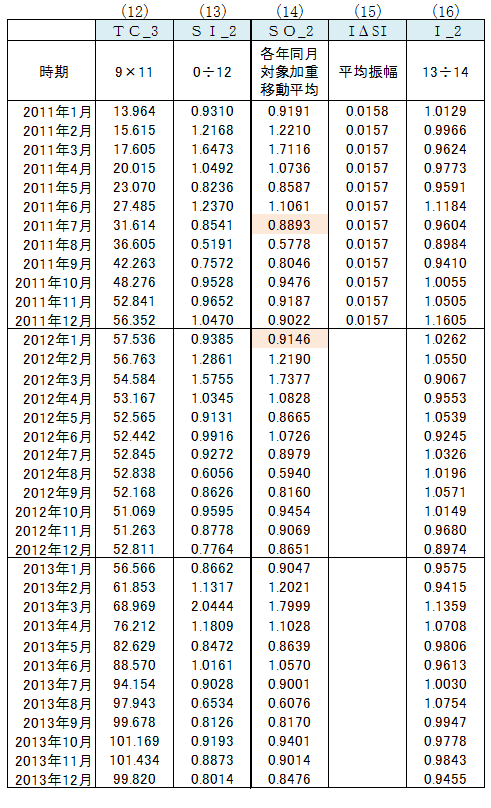
（１２）ＴＣ_3 ＴＣの近似値算出

（9）のＴＣ_2 × （11）のＩ(ＴＣ) より、ＴＣの近似値ＴＣ_3を算出。

（１３）ＳＩ_2 ＳＩの近似値を算出

（0）のＴＣＳＩ ÷ （12）のＴＣ_3 より、ＳＩの近似値ＳＩ_2を算出。

（１４）ＳＯ_2 ＳＩの調整

（13）のＳＩ_2に7項の「各年同月対象加重移動平均」を適用しＳＯ_2を算出。

【計算例】

・2011年7月（4×2011年7月＋3×2012年7月＋2×2013年7月）÷9

＝（4×0.8541＋3×0.9272＋2×0.9028）÷9
＝0.8893　　　　　　

・2012年1月　（3×2011年1月＋4×2012年1月＋3×2013年1月）÷10

＝（3×0.9310＋4×0.9385＋3×0.8662）÷10
＝0.9146

（１５）ＩΔＳＩ　平均振幅を算出

（14）のＳＯ_2の各月の経年変化率から平均振幅を算出。

【計算例】　1月

①　(0.9047－0.9146)÷0.9047＝0.0109

マイナスはプラスとする

② (0.9146－0.9191)÷0.9146＝0.0050

平均振幅＝①＋②＝0.0109＋0.0050＝0.0158

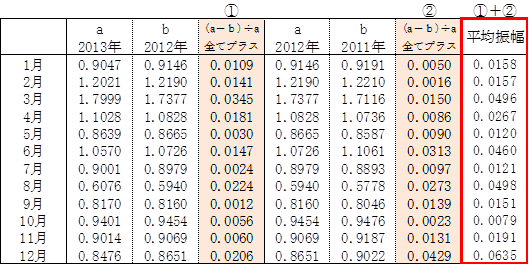
（１６）Ｉ_2 　Ｉの近似値を算出

（13）のＳＩ_2 ÷ （14）のＳＯ_2 より、Ｉの近似値Ｉ_2を算出。

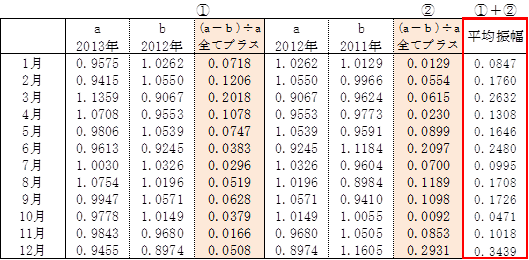
（１７）ＩΔＩＩ　平均振幅を算出

（16）のＩ_2の各月の経年変化率から平均振幅を算出。

【計算例】

1月

①(0.9575－1.0262)÷0.9575＝0.0718

マイナスはプラスとする

②(1.0262－1.0129)÷1.0262＝0.0129

平均振幅＝①＋②＝0.0718＋0.00129＝0.0847

（１８）ＭＳＲ　季節性変化率を算出

（17）のＩΔＩＩ ÷ （15）のＩΔＳＩより、季節性変化率ＭＳＲを算出。

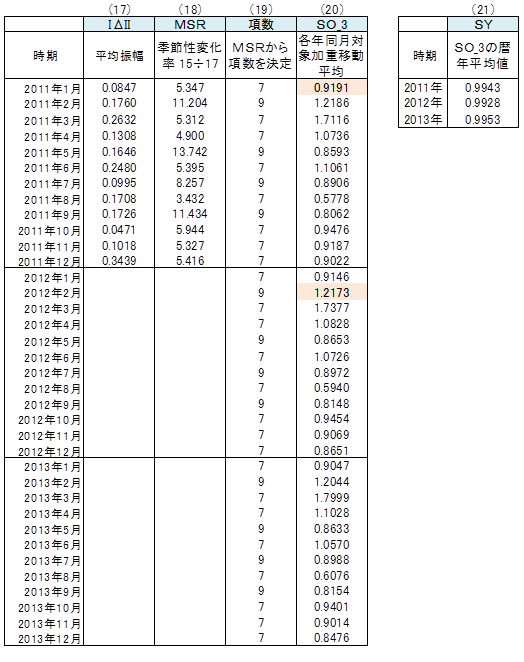
（１９）項数の決定　各年同月対象加重移動平均の項数を決定

（20）のＳＯ_3の算出は「各年同月対象加重移動平均」を適用するが、その際の項数はＭＳＲの大きさによって決める。

ＭＳＲ＜1.5・・・3項　　　1.5≦ＭＳＲ＜3・・・5項

3≦ＭＳＲ＜6・・・　7項　　　ＭＳＲ≧6・・・ 9項

（２０）ＳＯ_3 Ｓの調整

（13）のＳＩ_2に3項～9項のいずれかの「各年同月対象加重移動平均」を適用し、ＳＯ_3を算出。ただし、項数はＭＳＲの大きさによって決める。

注.ＭＳＲ(季節性変化率)が大きいＳＩ_2は、項数の大きい

「各年同月対象加重移動平均」を適用することにより、変動がより小さいＳＯ_3が求められる。

【計算例】

・2011年1月 7項

（4×2011年1月＋3×2012年1月＋2×2013年1月）÷9

＝（4×0.9310＋3×0.9385＋2×0.8662）÷9
＝0.9191

・2012年2月 9項

（4×2011年2月＋5×2012年2月＋4×2013年2月）÷13

＝（4×1.2168＋5×1.2861＋4×1.1317）÷13
＝1.2173

（２１）ＳＹ　ＳＯ_3 の暦年平均値

各年のＳＯ_3 の平均値ＳＹを算出。

（２２）Ｓ　最終Ｓの算出

（20）のＳＯ_3 ÷ （21）のＳＹより、最終のＳを算出。

【計算例】

2011年1月　2011年1月ＳＯ_3÷2011年ＳＹ
＝0.9191÷0.9943
＝0.9244

2012年2月　2012年2月ＳＯ_3÷2012年ＳＹ
＝1.2173÷0.9928
＝1.2261

（２２）Ｓ　来年度のＳの予測

来年度のＳは公式によって予測する。
（3×最終年Ｓ－前年Ｓ)÷2

【計算例】

2014年1月　 (3×2013年1月－2012年1月)÷2　

＝(3×0.9090－0.9212)÷2＝0.9029

（２３）ＴＣＩ　最終ＴＣＩの算出

（0）のＴＣＳＩ ÷ （22）のＳより、最終のＴＣＩを算出。　　

（２４）ＴＣ_4　ＴＣの近似値算出

（23）のＴＣＩに「9項加重移動平均」を適用し、ＴＣ_4を算出。

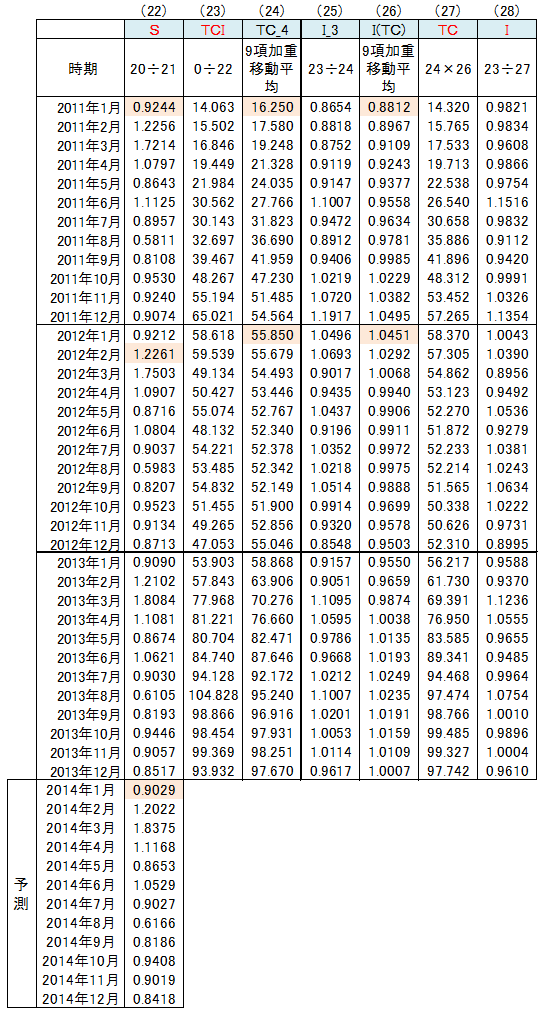
【計算例】

・2011年1月の9項加重移動平均

（5×2011年1月＋4×2011年2月＋3×2011年3月＋2×2011年4月＋2011年5月)÷15

＝（5×14.063＋4×15.502＋3×16.846＋2×19.449＋21.984）÷15

＝16.250

・2012年1月の9項加重移動平均

（2011年9月＋2×2011年10月＋3×2011年11月＋4×2011年12月＋5×2012年1月＋4×2012年2月＋3×2012年3月＋2×2012年4月＋2012年5月）÷ 25

＝（39.467＋2×48.267＋3×55.194＋4×65.021＋5×58.618+4×59.539＋3×49.134＋2×50.427＋55.074 ）÷25
＝55.850

（２５）Ｉ_3 Ｉの近似値算出

（23）のＴＣＩ ÷（24）のＴＣ_4 より、Ｉの近似値Ｉ_3を算出。

（２６）Ｉ(ＴＣ) Ｉの調整

（25）のＩ_3に「9項加重移動平均」を適用し、Ｉ(ＴＣ)を算出。

【計算例】

・2011年1月の9項加重移動平均

（5×2011年1月＋4×2011年2月＋3×2011年3月＋2×2011年4月＋2011年5月)÷15
＝（5×0.8654＋4×0.8818＋3×0.8752＋2×0.9119＋0.9147）÷15

＝0.8812

・2012年1月の9項加重移動平均

（2011年9月＋2×2011年10月＋3×2011年11月＋4×2011年12月＋5×2012年1月＋4×2012年2月＋3×2012年3月＋2×2012年4月＋2012年5月）÷25
＝（0.9406＋2×1.0219＋3×1.0720＋4×1.1917＋5×1.0496＋4×1.0693＋3×0.9017＋2×0.9435＋1.0437）÷25
＝1.0451

（２７）ＴＣ　最終ＴＣの算出

（24）のＴＣ_4 × （26）のＩ(ＴＣ) より、最終のＴＣを算出。

（２８）Ｉ　最終Ｉの算出

（23）のＴＣＩ ÷ （27）のＴＣより、最終のＩを算出。

＜＜前のページへ　　１　　２　　３